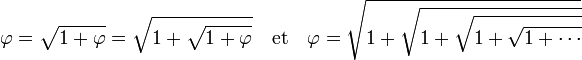Il est des mathématiciens qui marquent la culture mathématique. Vous connaissiez déjà sûrement Pascal, Descartes, Euler, Gauss… Mais connaissez-vous Galois ? Hormis le fait qu'il eût un prénom rare, que peut-il avoir de spécial ?

En 1823, à douze ans, il entre au collège-lycée Louis-le-Grand à Paris et se passionne rapidement pour les mathématiques. Il dévore les ouvrages de Legendre, Gauss et Lagrange, réussit le Concours général. La « fureur des mathématiques qui le domine » l'amène à se présenter au concours de l'École polytechnique à l'été 1828. Malheureusement, il échoue.
L'année suivante, son professeur fait publier un de ses articles dans les Annales de mathématiques pures et appliquées de Gergonne, l'un des premiers grands périodiques de mathématiques. La même année, il propose un mémoire sur la théorie des équations à l'Académie des sciences. Enfin, il retente sa chance à Polytechnique mais passe également le concours de l'École préparatoire, aujourd'hui l'École normale supérieure (ENS) de la rue d'Ulm, à Paris. Refusé à l'X mais accepté à l'ENS, il rejoint cette dernière après obtention de ses deux baccalauréats (allez savoir) en 1830 à dix-huit ans.

Durant les deux années qui suivent, Galois proposera nombre de travaux mais faute d'être complets ou par malchance, ils ne sont pas publiés. Augustin Cauchy et Siméon Poisson, deux grands mathématiciens, retardent ses publications dans l'objectif d'obtenir une théorie plus complète, parfois tout simplement sans raison. Cette théorie ne viendra pas. Pourquoi ?

Après son engagement politique républicain qui le conduit régulièrement en prison, Évariste Galois rencontre une jeune femme à l'hôpital. Il en tombe amoureux mais ne semble pas heureux. Le 14 mai 1832, elle souhaite rompre et le 30 mai, il affronte en duel un de ses amis. Encore une fois, pourquoi ? Ce n'est pas très clair. Il pourrait s'agir de son rival en amour avec la jeune femme, ou bien le duel fut un « duel imbécile entre amis ». Dans tous les cas, Galois est touché à l'abdomen par la balle de son adversaire et meurt le lendemain. Il meurt à vingt ans.

Galois était connu pour son tempérament très fougueux. Lors d'un oral, il n'hésita pas à lancer une éponge à la tête de l'examinateur, qui ne comprenait pas sa démonstration. Pour faire simple, il ramenait souvent sa fraise, remettait sans cesse en cause l'ordre politique établi, ce qui l'a d'ailleurs conduit à être renvoyé de l'ENS en 1831. Il était donc de ces génies méconnus qui meurent jeunes, tels Niels Abel, un autre mathématicien de Norvège cette fois-ci, mort à 26 ans, peu avant de recevoir un prix avec Jacobi pour ses travaux.

Galois a principalement travaillé sur la théorie des équations (la résolution d'équations polynomiales, telles \(3x^5 + 4x^4 - 2x^3 + x^2 - x + 4 = 0\)) ainsi que sur les fractions continues, en voici un exemple simple :

\(\sqrt{13}=3+\cfrac1{1+\cfrac1{1+\cfrac1{1+\frac1{1+\frac1{6+\cdots}}}}}\)

Donnons un petit exemple avant de nous quitter. Vous connaissez sûrement le nombre d'or, \(\phi\), qui est le nombre tel que :

\(\phi^2 = \phi + 1\) puisque c'est la seule solution positive de l'équation \(x^2 - x - 1 = 0\).

Nous avons donc :

\(\phi = \sqrt{\phi + 1}\)

Nous pouvons remplacer le \(\phi\) sous la racine par sa propre valeur !

\(\phi = \sqrt{\sqrt{\phi+1} + 1}\)

Et ainsi de suite, à l'infini…