Blaise Pascal était un touche-à-tout, comme beaucoup d'hommes du XVIIe siècle : philosophe, physicien, et, dans le cas qui nous concerne ici, mathématicien. En effet, cet homme inspiré est à l'origine d'un objet mathématique à la fois intéressant et extrêmement pratique : le triangle de Pascal(1).

Il s'agit d'une formation particulière de nombres qui se construit très facilement : sur une première ligne, inscrivez 1. Nous allons numéroter cette première ligne 0 – vous verrez plus tard pourquoi pas 1. À la ligne juste en dessous, qui sera la ligne numéro 1, étendez le triangle en inscrivant un 1 un peu sur la gauche du premier, et un 1 un peu sur sa droite. Vous obtenez la figure suivante :

Deux lignes

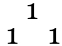
Vous allez continuer d'étendre le triangle à chaque ligne, en appliquant la règle suivante : chaque nombre que vous inscrirez sera égal à la somme des deux nombres juste au-dessus de lui, celui un peu sur sa gauche et celui un peu sur sa droite. Ainsi, vous voyez pourquoi nous avons inscrit deux 1 à la ligne numéro 1 : le premier se trouvait juste en-dessous d'un 1 et de rien du tout, idem pour le second. À l'étape suivante (ligne 2), vous obtenez donc :

Trois lignes

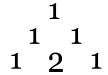
En effet, le 2 se trouvait juste en dessous de deux 1. Voici la ligne 3 :

Quatre lignes

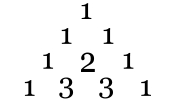
Chacun des 3 se trouve bien juste en-dessous d'un 1 et d'un 2. Pour les lignes 4 et 5, on obtiendra donc :

Six lignes

Et ainsi du suite, autant que vous le voulez. Une remarque : les nombres que vous obtenez en construisant une ligne du triangle de Pascal sont appelés « coefficients binomiaux », et ont plein d'autres applications, en algorithmique notamment. On note \({i \choose j}\) le coefficient binomial placé à la ligne \(i\) (toujours selon ma numérotation), et qui est le \(j\)ème nombre de la ligne(2). Ça, c'était pour votre culture ; je me servirai du terme « coefficients binomiaux » ici, mais pas d'\(i\) ou de \(j\).

Voilà, vous avez construit un triangle de Pascal. Cependant, je me doute qu'outre l'aspect « les maths, c'est rigolo », vous vous demandez à quoi cela peut bien servir. Eh bien, vous vous souvenez peut-être de ces formules que vous avez dû retenir en troisième, les fameuses identités remarquables, qui vous ont notamment servi à développer \((a+b)^2\) et \((a-b)^2\). Si ce n'est pas le cas, ou si vous n'êtes pas encore en troisième, voici un rappel :

\((a+b)^2 = a^2 + 2ab + b^2\)

\((a-b)^2 = a^2 - 2ab + b^2\)

Vous vous en doutiez peut-être, mais il existe des formules de même type, quoique beaucoup plus longues, pour développer, par exemple, \((a+b)^5\), et même n'importe quelle puissance de \((a+b)\). Le rapport avec le triangle de Pascal ? Ce dernier vous permet de trouver sans calculs monstrueux n'importe quelle formule développée de \((a+b)^n\) ! C'est là qu'entre en jeu la numérotation des lignes dont je vous parlais tout à l'heure, et ces fameux coefficients.

Pour développer \((a+b)^n\), construisez un triangle de Pascal jusqu'à la ligne \(n\). Recopiez quelque part la ligne \(n\), avec des espaces entre les coefficients. Ainsi, si je prends l'exemple de \((a+b)^5\), je dois construire mon triangle de Pascal jusqu'à la ligne 5, qui est la dernière ligne construite ci-dessus. Je recopie donc quelque part : \(1 5 10 10 5 1\). Maintenant, il ne reste plus qu'à rajouter des \(a\) et des \(b\), ainsi que des \(+\) ! Vous devez donc multiplier les coefficients binomiaux par des puissances de \(a\) descendant de \(n\) à \(0\), et des puissances de \(b\) montant de \(0\) à \(n\).

Qu'est-ce que cela veut dire ? Eh bien, juste derrière mon \(1\), j'écris \(a\) à la puissance \(n\) que je voulais tout à l'heure – \(5\) dans notre exemple. \(b\) est à la puissance \(0\), mais \(b^0\) vaut toujours 1, donc je n'écris rien (multiplier par 1 ne sert à rien). Nous avons donc \(1 \times a^5 \times b^0\), c'est-à-dire \(a^5\). Ensuite, je passe au coefficient suivant, un 5 : je le multiplie cette fois par \(a\) à la puissance 4, puisque ses puissances descendent, et par \(b\) à la puissance \(1\), puisque ses puissances montent. On a \(5a^4b^1\), donc \(5a^4b\). De la même manière, on obtient ensuite \(10a^3b^2\), et ainsi de suite. Finalement, on ajoute des \(+\) entre chaque « groupe » de la forme « coefficient multiplié par une puissance de \(a\) puis par une puissance de \(b\) » ainsi créé, et on obtient la formule magique :

\((a+b)^5 = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5.\)

Cela paraît un peu long, fait comme ça, mais en refaisant cela deux ou trois fois, vous aurez le coup de main et gagnerez un temps fou dès que vous vous retrouverez face à ce type d'identité remarquable.

Notez une première chose : cette technique marche également avec \((a-b)^n\), à ceci près qu'il faut rajouter une étape. Après le premier « groupe » \(a^nb^0\), alternez les – et les +. Pour la ligne 5, par exemple, on obtient :

\((a-b)^5 = a^5 - 5a^4b + 10a^3b^2 - 10a^2b^3 + 5ab^4 - b^5.\)

Seconde remarque : les trois premières lignes correspondent à des formules que vous connaissez bien :

  • À la ligne 0, on calcule \((a+b)^0\). On a un seul « groupe », de coefficient 1, et les puissances de \(a\) descendent de 0 à 0 et celles de \(b\) montent de 0 à 0. On a donc \((a+b)^0 = 1\times a^0\times b^0 = 1\). Or, vous le savez, tout nombre élevé à la puissance 0 est égal à 1 (sauf \(0\), car \(0^0\) n'est pas défini). Donc \((a+b)^0\) est bien égal à \(1\).
  • À ligne 1, vous avez \((a+b)^1 = 1\times a^1\times b^0 + 1\times a^0\times b^1 = a + b\). Logique, me direz-vous, que \((a+b)^1\) soit égal à \(a+b\) !
  • À la ligne 2, on obtient \((a+b)^2 = 1\times a^2\times b^0 + 2\times a^1\times b^1 + 1\times a^0\times b^2 = a^2 + 2ab + b^2\). Eh oui, vous avez bien retrouvé l'identité remarquable numéro 1 que vous connaissiez ! Vous constatez qu'avec la règle pour \((a-b)^2\), on retrouve également l'identité remarquable numéro 2 !

Eh bien, vous voilà bien parés pour développer des expressions monstrueuses, telle \((a+b)^9\), en un rien de temps ! N'oubliez pas, cependant, que cet outil est pour votre usage « personnel » ; un professeur appréciera peu de voir un « d'après le triangle de Pascal » sur une copie pour justifier un tel développement(3) !

  1. (1) ↑ Notez qu'on ne peut pas se tromper sur le nom de l'inventeur !
  2. (2) ↑ Et non pas \(j\)ème chiffre de la ligne, attention aux confusions !
  3. (3) ↑ Croyez-moi, j'ai essayé !