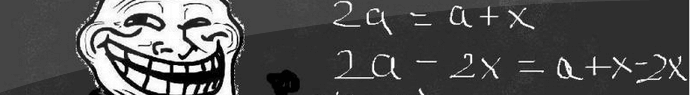
2 serait-il égal à 1 ?
Peut-on montrer que deux est égal à un ?
Vous venez juste de lire le titre de cet article et vous vous demandez sans doute quelle est cette étrange idée. Depuis toujours vous savez que \(1+1=2\) et que \(1\) est différent de \(2\), et pourtant…
Prenons deux nombres que l'on appellera \(A\) et \(B\) tels que \( A= B\).
Multiplions-les tous les deux par A :
\(A^{2} = AB\)
Soustrayons \(B^{2}\) :
\(A^{2}-B^{2} = AB-B^{2}\)
On reconnait une identité remarquable dans le membre de gauche, et on peut factoriser à droite, ce qui donne donc :
\((A+B)(A-B) = B(A-B)\)
Simplifions :
\(A+B = B\)
Or on avait dit au départ que A était égal à B, on a donc :
\(2B = B\)
Et en divisant par B on obtient bien :
\(2 = 1\)
Étrange, étrange, nous aurait-on menti depuis notre plus tendre enfance ?
Rassurez-vous chers lecteurs ce n'est pas le cas ou du moins on ne nous a pas menti à ce sujet-là.
Mais alors que s'est-il passé ? Comment a-t-on réussi à obtenir \(2 = 1\) par une suite d'opérations qui semblent pourtant valables ?
Regardez de plus près, reprenez une par une les opérations que nous avons effectuées. Alors vous avez trouvé ? Il y a bien une faute scandaleuse et votre professeur de mathématiques aurait eu une crise cardiaque en voyant ça. En effet à la cinquième ligne on a divisé par \((A-B)\) mais \(A\) étant égal à \(B\) cela signifie qu'on a divisé par zéro ce qui est formellement interdit.
Petit rappel ou petite explication pour ceux qui ignorent encore les raisons de cette impossibilité de diviser par zéro :
- Vous avez 10 billes et vous voulez faire 0 tas de billes, comment faites vous ? si vous laissez les billes telles qu'elles sont vous avez 1 tas, si vous les séparez vous avez entre 2 et 10 tas mais il est impossible de faire zéro tas (à moins de manger les billes ce qui n'est pas conseillé(1)).
- Écrit mathématiquement ça donne \(\frac{10}{0} = ?\). Supposons qu'il existe \(C\) tel que \(C = \frac{10}{0}\) alors on aurait \(C \times 0 = 10\) c'est à dire \(0 = 10\) ce qui est absurde.
Vous l'avez donc compris on ne divise jamais, jamais, jamais, au grand jamais, par zéro.
Ajoutons que si l'on transgresse une règle mathématique on peut obtenir tout et n'importe quoi alors prudence.
- (1) ↑ Remarque à l'attention des plus jeunes lecteurs et de ceux qui n'auraient pas compris que c'était ironique : ne mangez pas les billes, c'est dangereux.