Victor Hugo disait que l'horizon souligne l'infini.
Et pourtant, assimiler l'horizon à l'infini est une grave erreur… car il n'est pas si loin.

Petit rattrapage pour les cancres. L'œil humain peut en théorie porter à l'infini⁽¹⁾ : si l'on ne peut pas voir notre dos en regardant au loin, c'est tout simplement parce que la Terre est ronde… et c'est cette courbure qui nous empêche de voir à l'infini.

Aujourd'hui, intéressons-nous à la distance de cet horizon. Bonne nouvelle : pas besoin d'être un grand scientifique pour comprendre, il suffit de se souvenir du théorème de Pythagore.
Posons les choses à plat comme d'habitude, ça ira mieux après : on va considérer la distance en mer (s'il faut prendre en compte les reliefs, on n'est pas sorti d'affaire), pour un humain de taille moyenne (1 m 73 en France, 1 m 62 sur le globe : soyons chauvins et prenons 1 m 73, soit une distance des pieds aux yeux d'1 m 65 environ).

Histoire d'expliciter, prenons la jolie image que vient de me dessiner Licoti :

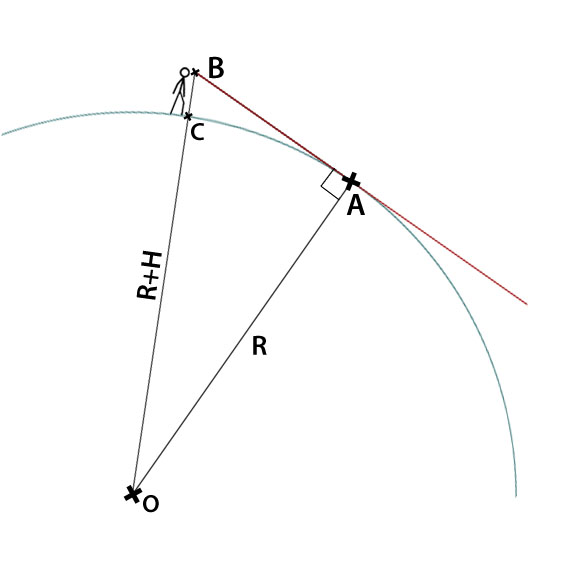
À l'horizon, le regard est tangent au globe : nous avons notre triangle rectangle. Puisque « le carré de l'hypoténuse bla bla bla », on obtient \(R^2 + d^2 = (R+h)^2\), avec, comme vous l'avez probablement compris, \(R\) le rayon de la Terre, \(h\) la taille de l'observateur, et \(d\) la distance de l'horizon. On manipule tout ça pour obtenir \(d = \sqrt{R^2 + 2Rh + h^2 - R^2} = \sqrt{2Rh+h^2}\).
Mais ne vous faites pas d'illusions : aussi grand que vous soyez, vous restez parfaitement négligeables devant le rayon de la Terre. On peut donc enlever le \(+h^2\) sans perdre en précision, et en déduire que l'horizon se situe à \(\sqrt{2Rh}\)km.
Maintenant, le calcul. On a le rayon de la Terre (\(R = 6367 km\)), et la hauteur de nos yeux (\(h = 0.00162 km\)). Aussitôt dit, aussitôt fait : \(d = 4.54km\)⁽²⁾. Vous voyez bien qu'il n'est pas à l'infini !

---

1. ⁽¹⁾ ↑ Au sens mathématique, en pratique il y a un moment où l'œil s'embrouille !
2. ⁽²⁾ ↑ Juste pour information, si on n'avait pas fait l'approximation de supprimer le \(+h^2\), on trouve un mètre d'écart au total. Largement négligeable par rapport à la valeur finale et aux autres approximations (rayon de la terre, hauteur des vagues…)