Avant de lire cet article, assurez-vous d'avoir lu l'épisode précédent !

Max⁽¹⁾ Planck, physicien des XIX^e et XX^e siècles, est notamment connu pour avoir émis la théorie des quanta en 1900. Cette théorie sera reprise par Albert Einstein cinq ans après. Planck en obtiendra un prix Nobel en 1918.

Sa théorie stipule que l'énergie d'une particule est composée de quanta⁽²⁾. Les particules composant une onde ont donc une énergie, notée \(E\), et définie par la formule suivante :

\(E = h \times \nu\)

\(\nu\)⁽³⁾ est la fréquence de l'onde, \(h\) est une constante, définie par Planck lui-même, et qui est donc la troisième constante fondamentale en physique, la constante de Planck :

\(h = 6,626 \times 10^{-34} J.s\)

\(h\) est parfois trouvée sous sa forme réduite, \(\hbar\) :

\(\hbar = \frac{h}{2\pi} = 1,05 \times 10^{-34} J.s\)

La fréquence \(\nu\) peut, quant à elle, s'exprimer de deux manières⁽⁴⁾ :

\(\nu = \frac{c}{\lambda} = \frac{1}{T}\)

Où \(c\) est la célérité de l'onde, \(\lambda\) sa longueur d'onde, dans le cas d'une onde se propageant. De manière générale, on utilise l'inverse de \(T\), la période de l'onde, mais les deux formules ne sont pas incompatibles, au contraire.

On peut d'ailleurs déduire quelque chose d'amusant :

\(\frac{cT}{\lambda} = 1\)

\(cT = \lambda\)

À présent, nous allons voir un exemple d'application de l'équation :

\(E = h \times \nu\)

Pour ce faire, nous allons prendre le cas de la lumière se propageant dans le vide (ou ailleurs, peu importe). Prenons donc la première définition de \(\nu\) et insérons-la dans l'équation précédente :

\(E = h \times \frac{c}{\lambda}\)

Or, dans le cas de la lumière, \(c\) est la célérité de… la lumière ! Rappelez-vous, nous avions défini \(c\) dans le premier article de cette série :

\(c = 2,997 \times 10^8 m.s^{-1}\)

\(c\) et \(h\) sont connus, on en déduit donc que :

\(E = 6,626 \times 10^{-34} \times \frac{2,997 \times 10^8}{\lambda}\)

\(E = \frac{1}{\lambda} \times 1,986 \times 10^{-25}\)

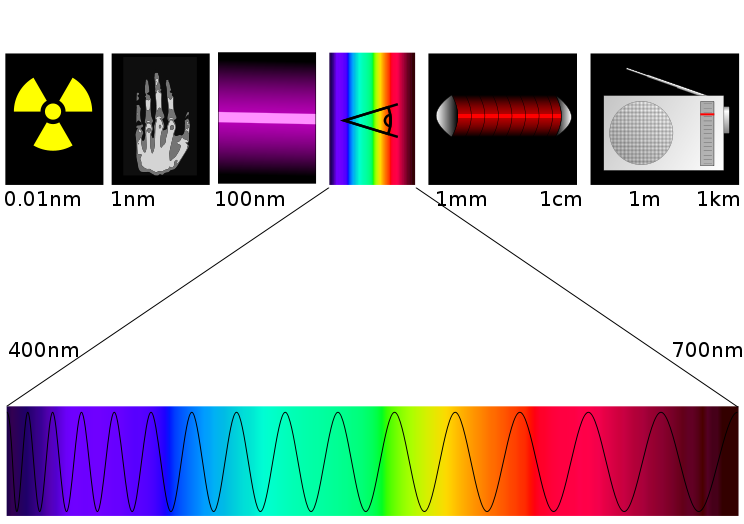
Pour finir, calculons les bornes d'un encadrement de l'énergie des photons composant la lumière visible. Celle-ci va du rouge au violet, soit de 780 nm à 446 nm⁽⁵⁾. Remarquez que plus la longueur d'onde est petite, plus l'énergie est grande.

On peut donc calculer \(E_{min}\) et \(E_{max}\) :

\(E_{min} = \frac{1}{780 \times 10^{-9}} \times 1,986 \times 10^{-25} = 2,547 \times 10^{-19} J\)

\(E_{max} = \frac{1}{446 \times 10^{-9}} \times 1,986 \times 10^{-25} = 4,454 \times 10^{-19} J\)

Dernière chose, nous allons convertir ces résultats en électron-volts, eV. Cette unité de mesure d'énergie (à ne pas confondre avec les volts (V)), est utilisée pour exprimer à notre échelle des valeurs d'énergies microscopiques. Pour le comprendre, il suffit d'en voir sa définition :

\( 1 eV = 1,602 \times 10^{-19} J\)

Un simple produit en croix nous donne \(E_{min}\) et \(E_{max}\) en électron-volts. Pour les différencier des valeurs données en joules, on va nommer ces nouvelles valeurs \(E_{Min}\) et \(E_{Max}\) :

\(E_{Max} = \frac{E_{min}}{1,6 \times 10^{-19}} = \frac{2,547 \times 10^{-19}}{1,602 \times 10^{-19}} = 1,59 eV\)

\(E_{Max} = \frac{E_{max}}{1,6 \times 10^{-19}} = \frac{4,454 \times 10^{-19}}{1,602 \times 10^{-19}} = 2,78 eV\)

D'où l'encadrement de l'énergie de la lumière visible – nommons-la \(E_L\) –, défini par \(E_Min\) et \(E_Max\) :

\(E_{Min} \leq E_{L} \leq E_{Max}\)

\(1,59 eV \leq E_{L} \leq 2,78 eV \)

Je vous quitte sur ce superbe schéma extrait de Wikipédia :

---

1. ⁽¹⁾ ↑ Max Karl Ernst Ludwig.
2. ⁽²⁾ ↑ Au singulier, un quantum, c'est-à-dire la plus petite mesure indivisible de l'énergie (un paquet élémentaire d'énergie en somme).
3. ⁽³⁾ ↑ La lettre grecque correspondant au n.
4. ⁽⁴⁾ ↑ Elle est notée \(f\) lorsqu'elle n'est pas spécifique à cette équation.
5. ⁽⁵⁾ ↑ Rappel : \(1 nm = 10^{-9} m\)

Cet article vous a plu ? Courez lire la suite !