Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 seconde.

Comment en est-on arrivé à cette définition ? Pour le savoir, et comme à chaque fois que l'on parle de physique ou d'astronomie, il faut remonter à l'Antiquité.

Dès le V^e siècle, l'ingénieur et philosophe grec Empédocle s'intéressa à la vitesse de la lumière, mais ne produisit que des spéculations. L'arabe Alhazen⁽¹⁾ ne parvient pas non plus à un résultat probant sur le calcul de cette constante de la physique, \(c\). Pourtant, durant sa vie s'étalant du X^e siècle au XI^e siècle, il a inspiré certains scientifiques du Moyen Âge⁽²⁾ et de la Renaissance, dont les brillants Johannes Kepler et ses trois lois, ainsi que Roger Bacon⁽³⁾, quelques siècles plus tôt. Ce dernier n'obtiendra pas de résultats plus concluants que son inspirateur musulman au sujet de la célérité de la lumière. Galilée, qui a pourtant démontré que la Terre tournait autour du Soleil⁽⁴⁾, s'y essaiera aussi, sans succès.

Il faudra attendre Ole Christensen Rømer, un danois du XVII^e siècle, qui travaillera sur les éclipses de Io, un satellite de Jupiter. Ses calculs — à savoir la position de Io, pour déterminer quand auraient lieu les éclipses – réalisés à l'aide des lois de Kepler⁽⁵⁾ –, seront parfois tout à fait pertinents, mais parfois non. Il trouvera un décalage : tantôt dix minutes de retard, tantôt dix minutes d'avance. C'est lors d'une démonstration, le 9 novembre 1676, qu'il se rend célèbre en prédisant les dix minutes de décalage. Le problème est l'imprécision du calcul, car le rayon de l'orbite terrestre (qui sert forcément pour le calcul des positions de la Terre et du Soleil) est mesuré de manière imprécise, allant de 68 à 138 millions de kilomètres : ces valeurs sont fausses⁽⁶⁾. Plus tard, Rømer trouvera un décalage de sept minutes.

L'impulsion donnée par ses mesures pousse Cassini et Newton à continuer la recherche et les mesures ; Jean-Baptiste Delambre trouvera huit minutes treize secondes, au lieu des huit minutes neuf secondes en réalité. Il n'était pas loin ! C'est au XIX^e siècle que tout se met en marche et que le calcul de la vitesse de la lumière se rapproche des valeurs réelles. Hippolyte Fizeau trouve, lors d'une expérience entre Suresnes et Montmartre, en 1849, 315 000 km. s^-1, soit une marge d'erreur de 5%⁽⁷⁾ !

Tout s'enchaîne et, en 1983, la Conférence des poids et mesures donne la définition du mètre à partir de la valeur de la célérité⁽⁸⁾ de la lumière, mentionnée au début :
Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 seconde. ⁽⁹⁾

On en déduit réciproquement \(c\), la célérité de la lumière dans le vide :

\(c = 299 792 458 m.s^{-1}\)

Cette constante de physique fondamentale, la première que l'on étudie aujourd'hui, sert dans de nombreuses équations très connues. La plus célèbre est sûrement celle d'Einstein, qui dit que tout corps possède une énergie (dans le cadre de la relativité restreinte) notée \(E\) telle que :
\(E = mc^2\)
Où \(m\) est la masse de l'objet et \(c\) la célérité de la lumière. On peut, par exemple, dresser un petit schéma de diverses énergies :

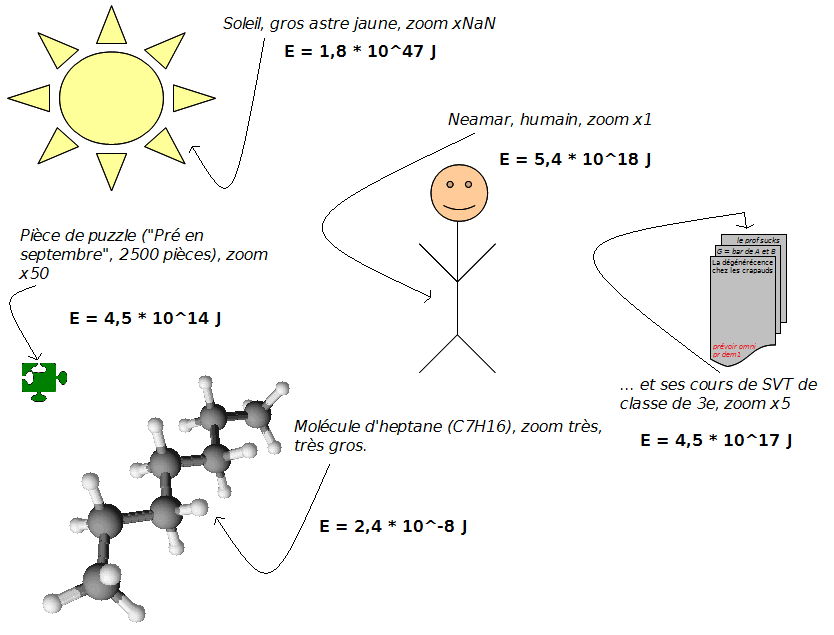
Il y a une autre équation dont nous allons parler : celle de la transformation de Lorentz.
Par exemple, lorsque deux voitures roulent en sens opposé et qu'elles vont l'une vers l'autre à 60 km. h^-1, on peut dire que chaque voiture verra l'autre arriver à \(60 + 60\), 120 km. h^-1. Cependant, on s'est rendu compte que ce genre de calculs donnait des résultats aberrants et médiocres dans des ordres de grandeurs plus grands. Cette formule d'addition n'est pas exacte, et c'est Lorentz qui s'est chargé de fournir une formule parfaite, qui s'exprime en fonction de la célérité de la lumière – là est l'intérêt :

\(u = \frac{v + w}{1 + \frac{vw}{c^2}}\)

Où \(u\) est cette vitesse perçue (dans notre cas, 120 km. h^-1), \(v\) et \(w\) les vitesses de nos deux bolides, \(c\) la célérité de la lumière.

Appliquons la formule dans notre exemple :

\(u = \frac{60 + 60}{1 + \frac{60 \times 60}{299792458^2}} = 119,999...\)

On a donc bien nos cent vingt kilomètres par heure ! Que se passe-t-il pour que l'on trouve la même chose ?
Si vous analysez la formule, vous remarquerez que le dénominateur a cette forme : \(1 + \frac{vw}{c^2}\). Or, \(c\) est très grand et mettre sa valeur au carré n'arrange pas les choses ! \(v\) et \(w\) sont de plus très petits, puisque ce sont de ridicules « 60 » (la différence d'ordre de grandeur est de presque 17, quand même⁽¹⁰⁾). Donc, lors de la division, \(\frac{vw}{c^2}\) vaut presque 0, en ajoutant à 1, on trouve que le dénominateur vaut à peu près 1. Et \(\frac{120}{1} = 120\)…

\(u = v + w = \frac{v + w}{1}\)

Voilà donc la fin de cet omnilogisme sur la première des grandes constantes fondamentales de la physique : la célérité de la lumière.

---

1. ⁽¹⁾ ↑ De son vrai nom Abū ʿAlī al-Ḥasan ibn al-Ḥasan ibn al-Haytham.
2. ⁽²⁾ ↑ Certainement pas français, je vous laisse deviner pourquoi.
3. ⁽³⁾ ↑ Ce moine, méconnu et horriblement persécuté pendant sa vie, est la plus grande figure scientifique du Moyen Âge. C'est le génie le plus vaste et le plus complet qui, dans cette longue période, se soit produit en Europe. en dira Louis Figuier, Montpelliérain vivant au XIX^e siècle.
4. ⁽⁴⁾ ↑ CIC Assurances le rappelle également dans sa publicité : Parce que le monde bouge.
5. ⁽⁵⁾ ↑ Notre cher astronome du SERG (Saint-Empire romain germanique) aura finalement été utile dans cette histoire.
6. ⁽⁶⁾ ↑ La valeur réelle est 149 millions de kilomètres
7. ⁽⁷⁾ ↑ \(\frac{299792458}{315000000} \times 100 \simeq 5\% \)
8. ⁽⁸⁾ ↑ Pour rappel, la célérité est la vitesse d'une onde, tandis que la vitesse est la vitesse d'un corps. Dans le cas de la lumière, les deux se disent, car les photons qui la composent sont de la matière, bien qu'ayant une masse nulle, et s'exprimant au niveau microscopique par un phénomène ondulatoire.
9. ⁽⁹⁾ ↑ En effet, par calcul on trouve que : \(c \times \frac{1}{299 792 458 s} = \frac{299 792 458 m.s^{-1}}{299 792 458 s} = 1m\)
10. ⁽¹⁰⁾ ↑ \(c^2 - 60 \simeq 8,9 \times 10^{16}\)

Cet article vous a plu ? Courez lire la suite !