En algèbre, nous appelons un carré, ou plus précisément un carré parfait, tout nombre entier élevé au carré ; c'est à dire à la puissance 2. Par exemple, 4 est un carré, car \(2^2 = 4\). Mais d'où vient cette appellation ?

Ces nombres ont été ainsi dénommés parce qu'ils peuvent justement être représentés sous la forme d'un carré plein.
Dans notre précédent exemple, 4 sera dit un carré car ce nombre peut être représenté par un carré de côté 2.
Ainsi, la suite des nombres carrés sera donnée par l'expression \(C_n = n^2\).

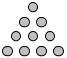
Si la dénomination des nombres carrés provient de la forme qu'ils créent étant assemblés par unités, celle des nombres triangulaires a des origines quasi similaires : les nombres triangulaires sont formés par des assemblages en forme de triangles équilatéraux. Les premiers termes de cette suite sont : \(1, 3, 6, 10, 15, 21\)…
La formule de cette suite est donnée par : \(T_n = \frac{n(n+1)}{2}\).

Vous aurez compris le principe. Il existe maintenant une infinité de telles suites, étant différenciées des autres par la forme géométrique que prennent leurs termes une fois assemblés. Nous en citerons par exemple les nombres pentagonaux, octogonaux, décagonaux. Ces ensembles de nombres forment ce qu'on appelle les nombres polygonaux.