
142 857
La magie des nombres phénix
Tout d'abord, qu'est-ce qu'un nombre phénix ? Un nombre phénix, aussi appelé nombre cyclique, est un nombre « dont les permutations circulaires des chiffres correspondent aux multiples du nombre »(1). Pour les incompétents notoires en mathématiques qui en apprécient toutefois la beauté, voici d'emblée l'exemple le plus connu : \(142 857\). Voyez ce qui se passe lorsque qu'on le multiplie par les chiffres de 1 à 6 :
- \(1 \times 142 857 = 142 857\)
- \(2 \times 142 857 = 285 714\)
- \(3 \times 142 857 = 428 571\)
- \(4 \times 142 857 = 571 428\)
- \(5 \times 142 857 = 714 285\)
- \(6 \times 142 857 = 857 142\)
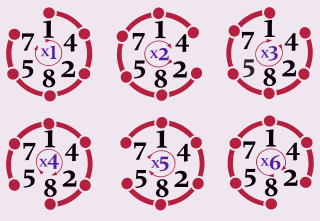
On remarque que chacun des résultats est le nombre du départ dont les chiffres sont décalés d'un ou deux crans, c'est donc pourquoi ces nombres sont appelés nombres cycliques.
Ce nombre provient des décimales de la division de 1 par 7 (\(\frac17 = 0.142857142857142857\) et ainsi jusqu'à l'infini).
Mais alors que se passe-t-il lorsqu'on les multiplie par 7 ? \(142857 \times 7 = 999999\)(2).
Le fait que les chiffres soient décalés lors de multiplications de 1 à 6 n'est pas le seul fait marquant ; il y a aussi des liens du même genre lorsque ce chiffre est multiplié par des nombres de 8 à 14, ou de 15 à 21(3). Intéressons-nous en revanche au carré de \(142 857\) : \(142857^2 = 20 408 122 449\).
Si l'on coupe le résultat en deux parties (20 408 et 122 449) :
\(20 408 + 122 449 = 142 857\) et revoilà notre nombre de départ.
Maintenant divisons-le en quatre parties (20, 408, 122 et 449) :
\(20 + 408 + 122 + 449 = 999\).
Par ailleurs, lorsque l'on forme trois groupes de nombres avec le chiffre de départ (14, 28 et 57) et qu'on les additionne :
\(14 + 28 + 57 = 99\).
Même chose lorsque l'on fait deux groupes de trois (142 et 857)
\(142 + 857 = 999\).
Vive la magie des mathématiques. 142 857 n'est pas le seul nombre cyclique. Les autres sont donnés eux aussi par l'inverse de certains nombres premiers comme 17, 19, 23 ou encore 47.