Peut-être avez-vous déjà entendu parler d'une étrange histoire : lorsqu'on vide son lavabo, un tourbillon se forme, et dont le sens de rotation dépendrait de l'hémisphère dans lequel on se trouve : dans l'hémisphère Nord, l'eau tournerait dans le sens anti-horaire, et dans l'hémisphère Sud dans le sens horaire. Parfois invoque-t-on même une cause à cela : c'est, dit-on, la faute à la force de Coriolis. Oui… Mais non. Pour commencer à s'en rendre compte, une simple question : dans quel sens tournerait l'eau d'un lavabo situé juste au-dessus de l'équateur ?

Faisons donc une mise au point. Pour commencer, qu'est-ce que la force de Coriolis selon vous ? Une force ? Raté. Enfin presque : la force de Coriolis est ressentie comme une force, car du fait que nous sommes en rotation autour du centre de la Terre, nous avons tendance à interpréter comme force ce qui ne l'est pas nécessairement⁽¹⁾. La force centrifuge en est un exemple : ce n'est pas vraiment une force (dans un manège qui tourne vite, rien ne nous pousse vers l'extérieur), et pourtant on la ressent (on est bien poussé vers l'extérieur).

Pour comprendre la force de Coriolis, place aux travaux pratiques : munissez-vous d'une raquette et d'une balle de tennis, et achetez-vous un billet pour le pôle Nord. C'est bon ? Faites à présent le meilleur service de votre vie, histoire d'envoyer la balle à quelques milliers de kilomètres. Observons à présent la trajectoire de la balle, en tenant compte de la rotation de la Terre :

Nous voyons ici la trajectoire de la balle depuis l'espace. Depuis la Terre, cependant, c'est autre chose :

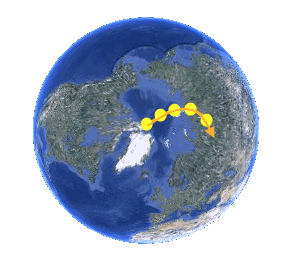
Ainsi, depuis la Terre, la balle de tennis aura été déviée, par une force, vers la droite de sa direction d'origine : dites bonjour à la force de Coriolis (Bonjour force de Coriolis !)⁽²⁾.

Plus généralement, la force de Coriolis dévie un objet lancé depuis l'hémisphère Nord vers la droite, et un objet lancé depuis l'hémisphère Sud vers la gauche. On pourrait donc se dire⁽³⁾ que la force de Coriolis fait bien tourner l'eau des lavabos, de même que les balles de tennis.
Sauf que l'on n'a pas encore vu le plus important : la valeur numérique. L'accélération que subit l'eau par la force de Coriolis vaut \(a_{C} = 2 \times \omega \times v \times |sin(l)|\), où \(\omega\) désigne la vitesse angulaire de la Terre (la vitesse de sa rotation sur elle-même), et vaut \(\omega \approx 7,29 \times 10^{-5} rad/s\) ; \(v\) la vitesse de l'objet étudié ; et \(l\) la latitude.

Avec cela, pour \(l = 45°\) (la latitude moyenne de la France) et \(v = 1 m/s\), on a \(a_C \approx 0.000103 m/s^2\), c'est à dire trois fois rien. Le Soleil exerce une accélération soixante fois plus importante sur le même lavabo⁽⁴⁾ !

Qu'on se garde cependant de dire que la force de Coriolis n'a aucun effet : sur des objets à masse beaucoup plus conséquente, la force de Coriolis se fait sentir⁽⁵⁾ : si vous avez un lavabo de plusieurs dizaines de milliers de litres, alors vous la verrez (peut-être) entrer en action.

Vous pouvez maintenant ravir la vedette à tous ceux qui reviennent d'un voyage dans l'autre hémisphère.

---

1. ⁽¹⁾ ↑ Ces « forces imaginaires » sont appelées forces inertielles.
2. ⁽²⁾ ↑ Cependant, la force de Coriolis n'est pas réduite à ce phénomène ; elle entraîne par exemple un décalage vers l'Est pour tout objet tombant, et un décalage vers l'Ouest pour tout objet montant.
3. ⁽³⁾ ↑ Et encore, ce n'est pas tout à fait pertinent…
4. ⁽⁴⁾ ↑ À titre de comparaison, l'accélération due à la gravité terrestre vaut environ 9,81 m/s². La force de Coriolis n'a donc aucun impact sur l'eau du lavabo.
5. ⁽⁵⁾ ↑ Car on a la relation \(F_C = m \times a_C\) : plus la masse est grande, plus la force de Coriolis est importante.