N'avez-vous jamais frémi devant un film Spider-Man ? N'avez-vous jamais craint la chute de votre héros favori ? Ne vous êtes-vous jamais accroché au bras de votre petite amie ou fermé les yeux jusqu'à ce que l'Homme-Araignée ne retrouve la terre ferme⁽¹⁾ ? Moi oui ! Et lorsque ces longues minutes d'effroi se prolongeaient en terribles insomnies, je me mettais à mon bureau et griffonnait, sur un coin de cahier, à la lueur de la bougie⁽²⁾ des formules qui permettraient définitivement de mettre notre sauveur à l'abri de la chute inéluctable et de l'écrasement bouilliesque auxquels il était promis. Je vais donc vous livrer ici les résultats de ces recherches passionnées.

Il est communément accepté que la toile d'araignée a une résistance environ 10 fois plus grande que l'acier et 3 fois plus grande que le kevlar. En fonction des valeurs de résistance mécanique en traction trouvées dans les tables, on peut dire que globalement l'acier à une résistance à la rupture en traction d'environ \(400/500 MPa\) et le kevlar d'environ \(3000 MPa\). On pourrait donc approximer que la toile d'araignée a une résistance à la traction comprise entre \(5000 MPa\) et \(10000 MPa\). Ne voulant prendre aucun risque pour la vie de mon héros, je prendrai la valeur minorante, soit \( 5000 MPa\).

Partant de là, et sachant que \(1 MPa = 1N/mm^2\) on peut dire que le fil d'araignée auquel est suspendu Spider-Man a une résistance limite à la traction d'au moins \(5000 N/mm^2\) soit \(500 kg/mm^2\). Chaque millimètre carré de cette soie peut donc supporter jusqu'à \(500 kg\).

Alors combien de kilogrammes peut supporter la toile de notre cher Spider-Man ? Ne connaissant pas avec exactitude le diamètre dudit fil, j'ai cherché à le calculer le plus précisément possible, et avec une rigueur mathématique dont vous seuls pourrez apprécier toute l'ampleur :

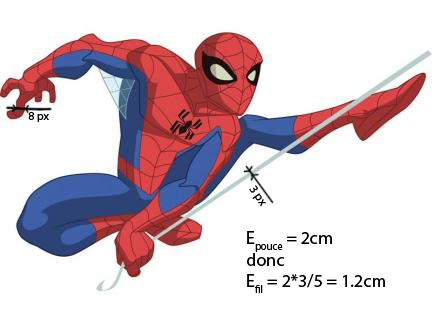
Ainsi donc, l'épaisseur de la toile d'araignée produite par Spider-Man serait de \(1.2 cm\) soit une surface de section de \(1.2^2 \times \pi = 4.5 cm^2 = 450 mm^2\).

Ainsi, la vie de notre héros ne tient qu'à un fil… mais un fil capable de supporter \(450*500 = 225000 kg = 225 tonnes\) !
Cette capacité semble bien suffisante, mais ce raisonnement n'est-il pas un peu biaisé⁽³⁾ ? Eh bien si me direz-vous, car Spider-Man ne fait pas que se suspendre, très souvent il chute avant de se rattraper.

Il convient d'intégrer dans ce calcul la notion de chute et de force exercées sur le câble afin de parfaire le raisonnement. Imaginons que notre homme tombe de la plus haute tour du monde⁽⁴⁾ : \(828 m\), et qu'il projette sa toile au dernier instant – ce serait tellement hollywoodien, mais imaginons un court instant cette improbable situation.
La deuxième loi de Newton, \( \sum \vec{\mathrm{F}}_{\mathrm{Oext/B}}(t) = m_{\mathrm{B}} \vec{a}_{\mathrm{B}}(t)\) nous apprend qu'une telle chute durerait \(t = \sqrt{2*828/10} = 12.9s\).
En effet, quand on lâche l'objet, si sa vitesse initiale est nulle, il parcourt en un temps \(t\) une distance égale à \(\frac{1}{2}gt^2\) et, l'accélération de pesanteur étant de \(9.81 m.s^{-2}\), chaque seconde augmentera la vitesse de chute du corps de \(9.81 m.s^{-1}\). Arrivé au niveau du sol, notre homme-araignée aura donc une vitesse de \(126.5 m.s^{-1}\). À partir de là, on peut en déduire l'accélération subie au pied de la tour :

\(a = \frac12 \times v^2 = 8000 m.s^{-2}\)

On peut alors dire abusivement que Spider-Man « paraitra » environ 800 fois plus lourd⁽⁵⁾ au pied de la tour qu'avant sa chute. Un homme normal pèse environ 80 kg⁽⁶⁾, ce qui équivaut à 64 tonnes au pied de l'immense gratte-ciel. Donc même après une chute de plus de 800 mètres, on est encore bien loin des 225 tonnes calculées précédemment. Ouf !
Cela laisse même un peu de marge pour rattraper des bus pleins d'enfants…
CQFD.

---

1. ⁽¹⁾ ↑ Sinon c'est que vous êtes un homme, un vrai !
2. ⁽²⁾ ↑ J'en fais trop ? C'est juste pour l'ambiance…
3. ⁽³⁾ ↑ Pour ceux qui n'auraient pas remarqué les multiples biais et simplifications de ce raisonnement.
4. ⁽⁴⁾ ↑ À Dubaï bien entendu – notre héros pourrait être amené à s'y rendre dans l'une de ses prochaines aventures.
5. ⁽⁵⁾ ↑ En réalité les forces de frottement dissipent de l'énergie tout au long de la chute par effet Joule et l'augmentation de la vitesse (l'accélération) ne sera pas constante tout au long des 828 m de descente.
6. ⁽⁶⁾ ↑ Tobey Maguire ne doit pas peser bien plus lourd que cela !