La loi de Benford (1)
Et si les chiffres se comportaient bizarrement ?
Quel est le point commun entre un long ticket de caisse du supermarché, un rapport de comptabilité pour une entreprise, et la liste des fleuves les plus longs au monde ? Réponse : ce sont tous trois des listes de nombres qualifiant chacune un type précis de données (des quantités d'argent dans les deux premiers cas, des longueurs dans le troisième). Quel intérêt, me direz-vous ?
L'intérêt, c'est qu'au cours du siècle dernier, plusieurs mathématiciens se sont aperçus d'un phénomène extrêmement étrange, qui touche précisément les longues listes de données numériques. Ce phénomène est appelé… Le Phénomène des Chiffres Significatifs ! *Musique horrifique* Quoi, vous n'avez pas peur ? Tant mieux après tout, dans ce cas nous pouvons nous attaquer sans crainte à ce mystère mathématique !
Tout commence en 1881, lorsque l'astronome américain Simon Newcomb s'aperçoit d'un détail tout bête : les pages des tables de logarithmes(1) les plus usées étaient les premières. Autrement dit, les gens regardaient bien plus souvent les logarithmes de nombres commençant par 1 que des autres.
Newcomb publia un article sur le sujet, mais fut complétement ignoré par la communauté mathématique. Un bon demi-siècle plus tard, Frank Benford, physicien, fait exactement la même observation. Seulement, cette fois, lui décide de creuser ses recherches et d'analyser d'autres données : des listes de longueurs de fleuves, les cours de la bourse, etc. Ses résultats expérimentaux l'amènent à cette conclusion pour le moins surprenante :
Dans une liste de données exprimées en une et une seule unité, les neuf chiffres significatifs possibles(2) ne sont pas répartis équitablement.
Incroyable, non ? Pourtant, il n'y a pas de raison particulière à cela : prenez les nombres 1 à 99 par exemple. Chaque chiffre significatif apparaît onze fois : une fois de 1 à 9, et dix fois dans sa dizaine (de 40 à 49 pour le 4 par exemple). Et pourtant, l'observation de Benford est vérifiée.
Faites l'expérience, chez vous. L'important est de mesurer le même type de grandeur. Voici quelques idées valables :
- Baladez-vous avec un mètre ruban chez vous, et mesurez la longueur d'une centaine d'objets (très différents si possible : un tube de tipex, votre télé, un verre, un rubik's cube), et notez les longueurs en centimètres dans une liste.
- Attendez que vos parents (ou vous) reviennent des courses du week-end avec un immense ticket de caisse (une centaine d'articles). Là, vous avez déjà la liste toute faite sous les yeux, c'est plus facile.
- Notez le nombre de pages d'un maximum de livres de chez vous.
Une fois votre liste faite, comptez le nombre de nombres commençant par 1, ceux commençant par 2, et ainsi de suite. Il y a de très fortes chances pour que les pourcentages d'apparition des différents chiffres ne soient absolument pas répartis équitablement.
Benford est même parvenu à mettre en équation la probabilité pour qu'un nombre commence par le chiffre \(d\) :
\(P_d = \log_{10}(1 + \frac{1}{d})\)
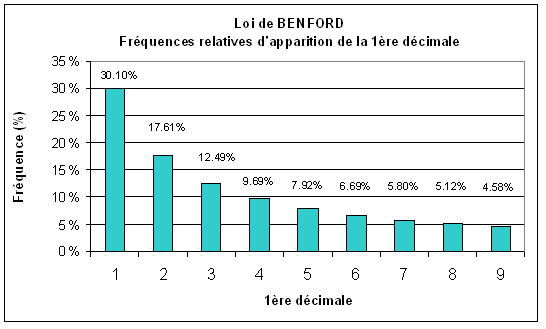
Mais plutôt que de s'embêter avec une formule compliquée et plus ou moins incalculable à la main, je vous propose les résultats pour chaque chiffre significatif, dans le graphique suivant :
Vous pouvez comparer avec vos résultats(3), il y a des chances pour que vos pourcentages ressemblent beaucoup à ceux du graphique !
Petite remarque : le graphique ne parle plus de probabilité, mais de fréquence, bien que l'on manipule les mêmes valeurs. La différence étant que la probabilité est la « chance » théorique pour qu'un chiffre apparaisse au début d'un nombre, tandis que la fréquence d'apparition d'un même chiffre est le pourcentage effectif de nombres commençant par celui-ci. Cependant, un principe appelé « théorie des grands nombres » veut que quand on reproduit une expérience mathématiques de probabilités (par exemple, tirer plusieurs fois un dé), plus on augmente l'échantillon testé, plus les résultats statistiques que l'on obtient se rapprochent des probabilités théoriques calculées.
Constatation importante : les chiffres sont répartis à des fréquences décroissantes, le 1 ayant nettement l'avantage (presque \(\frac{1}{3}\) de chances d'être chiffre significatif d'un nombre !), et le 9 culminant à un ridicule 4,58 %. Vous conviendrez qu'on est bien loin de la répartition de \(\frac{1}{9}\) pour chaque chiffre que s'imagine le bon sens, n'est-ce pas ?
Quant à l'explication de cet effet… il va falloir attendre le prochain article !
- (1) ↑ Au fait, qu'est-ce qu'une table de logarithme ? Petit indice : nous sommes en 1881, et les calculatrices coûtent beaucoup, voir énormément plus cher qu'une bête TI-83 d'aujourd'hui. Aussi, les étudiants en mathématiques, plutôt que d'investir dans un appareil hors de prix, préfèrent acheter ces petits livrets, qui contiennent les logarithmes de référence (de 1, de 2, de 3, etc.).
- (2) ↑ Le chiffre significatif d'un nombre est tout simplement celui par lequel commence le nombre. Exemples : 1 pour \(17,48\) ; 2 pour \(0,0267\) ; 3 pour \(3,1\) ; etc. Un nombre peut avoir pour chiffre significatif les chiffres de 1 à 9.
- (3) ↑ Obtention des pourcentages : pour chaque chiffre, divisez le nombre de fois où il commence un nombre par le nombre total de nombres que vous avez notés (ex : le nombre d'articles sur votre ticket de caisse), et multipliez le tout par 100. Faites cela pour chacun des neuf chiffres pour obtenir vos neuf pourcentages.