
Autour de la poussée d'Archimède
Comment fonctionne la poussée d'Archimède si on pèse aussi lourd que l'eau ?
Tout le monde connait la poussée d'Archimède dont une formulation classique est :
Tout corps plongé dans un fluide au repos subit de la part de celui-ci une poussée vers le haut de la valeur du poids de fluide déplacé.
Mais par ailleurs, vous savez sûrement aussi que la pression est une force qui s'exerce de toute part, par exemple sur les parois d'un aquarium ou la chambre à air d'un pneu de voiture.
Si je vous parle de tout cela, c'est parce que nous allons mélanger les deux sujets dans le contexte d'un petit exercice de flottabilité. Imaginons un bassin profond et rempli d'eau. Plaçons dans ce basin une colonne dont le disque de base fait 1m\(^2\) et de hauteur 10m. On la fabrique de telle sorte que sa masse volumique égale parfaitement celle de l'eau environnante et on la place verticalement de sorte que la surface supérieure corresponde exactement avec la surface de l'eau. La question est la suivante : une fois revenu à l'équilibre, de quelle hauteur la colonne dépasse-t-elle le niveau de l'eau ?
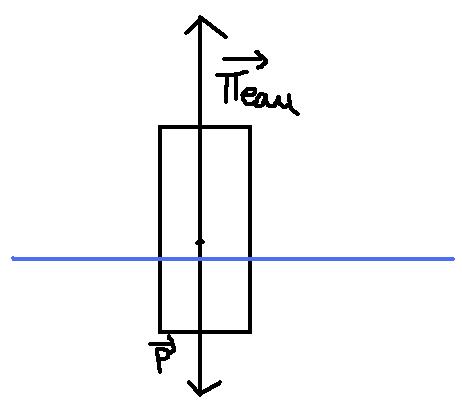
Mmmh, déjà la colonne dépasse-t-elle le niveau de l'eau ? Voyons voir, il est dit que la masse volumique de la colonne égale celle de l'eau. Donc la poussée d'Archimède, correspondant au poids du volume déplacé, compense exactement le poids réel de la colonne. De ce côté là, les forces s'équilibrent et n'ont aucune tendance à faire bouger la colonne. Mais par ailleurs, la colonne est particulièrement grande, il convient de prendre en compte la variation de pression entre la surface et les 10 m de profondeur. La pression s'exerçant sur les côtés de la colonne n'a aucune influence puisqu'elle est compensée de part et d'autre. On ne peut cependant pas en dire autant des surfaces de bases. En effet, la pression au niveau de la surface (atmosphérique, quelle que soit sa valeur) est inférieure à la pression à 10 m de profondeur. La force exercée sur le sommet de la colonne est plus faible que celle s'exerçant par le dessous, la colonne devrait donc avoir tendance à monter. Et le volume de la colonne qui dépasse ne déplaçant plus d'eau, la poussée d'Archimède diminuerait jusqu'à un équilibre qui compenserait la variation de pression entre le sommet et le fond de la colonne. Il ne reste plus qu'à déterminer cet équilibre. Cela sera facile moyennant quelques petites approximations.
On va prendre une masse volumique de l'eau de 1kg/L et négliger celle de l'air, il faut ensuite calculer la pression de l'eau en fonction de la profondeur. Ici, c'est facile aussi, on sait que la pression est linéaire, et on connait sa valeur en deux points : à la surface (pression atmosphérique) et à 10 m de profondeur (2 atmosphères, ordre de grandeur classique : +1atm tous les 10 m d'eau). La pression a donc pour valeur sous l'eau \(p=1+0.1 h\) en atmosphères où h est la profondeur en mètres de la base de la colonne. Du coup, la résultante de la pression vaut environ \(0.1 \times h \times 100 000 = 10 000 h N\)(1). Par ailleurs, comme la partie de la colonne qui dépasse de l'eau ne participe plus à la poussée d'Archimède (on la néglige dans l'air), le poids qui n'est plus compensé par Archimède vaut environ \(1000 \times 10 \times H = 10 000H N\) (Où H est la hauteur qui dépasse, à savoir \(10 - h\)). On a donc un équilibre à 5 mètres de profondeur, la moitié de la hauteur de la colonne !
Holà, pas si vite ! M'est d'avis que si on jette une colonne de 10 tonnes d'eau dans l'eau, elle ne va pas s'amuser à se dresser virilement. Alors, quelle erreur a-t-on commise ? Une petite idée ?
Le résultat devrait vous mettre la puce à l'oreille…
C'est parce qu'on a compté la poussée d'Archimède deux fois ! En fait, la résultante de la pression est la poussée d'Archimède. Cela se démontre très facilement de la manière suivante. La pression exercée sur un solide ne dépend que de la forme de celui-ci, pas de sa nature. Un solide plongé dans l'eau subit donc la même résultante de pression qu'une masse d'eau de même forme. Or une masse d'eau plongée dans l'eau n'a aucune tendance à bouger ! La résultante de pression compense donc exactement l'ensemble des autres forces appliquées à la masse d'eau, à savoir : son poids. On retrouve donc la formulation : une poussée d'Archimède de valeur le poids du liquide déplacé. La bonne réponse est donc que la colonne ne va pas dépasser de l'eau !
Mais alors, pourquoi se casser la tête à calculer la résultante de pression ? Eh bien parce que la poussée d'Archimède telle que dans sa formulation n'est valide que dans un seul cas très particulier : le corps en plongée dans un fluide au repos, alors que la résultante de pression est toujours valide.
Ainsi, si la colonne est collée au fond du bassin par exemple, il n'y a pas d'eau en dessous. La résultante de pression cette fois-ci la plaque au fond. C'est l'effet ventouse. Par ailleurs, tout se passe différemment quand le fluide (ou le solide, c'est pareil) n'est plus au repos. C'est ce qui fait voler des avions, et peut-être aussi couler les bateaux aux Bermudes à cause de forts courants. Vous avez peut-être déjà expérimenté ce dernier phénomène : il est plus difficile de flotter en présence de courants. Cela se remarque notamment si vous avez fait du canyoning(2). C'est pourquoi les gens qui se noient ne sont pas forcément des imbéciles qui ne savent pas nager. Prudence donc avec les courants, votre flottabilité n'est pas systématiquement assurée par le bon vieux Archimède.
