Maintenant que vous avez été converti par Et si on disait que aux joies des voyages dans le temps et à leurs apports substantifiques, je me propose d'appréhender la partie technique du projet – à savoir le voyage dans le temps à proprement parler. Pour simplifier les choses, je vais supposer que vous jugez le passé trop barbare pour y vivre ; vous allez donc faire un saut dans le futur, piquer une invention à quelque génie, revenir au temps présent et vous en attribuer le mérite.

Ce qui tombe bien, c'est qu'il est plus simple de voyager vers le futur que vers le passé, et pour cause ! vous le faites plus souvent que vous ne le pensez. Pour comprendre ce phénomène, nous aurons besoin d'une fusée, d'un faisceau laser lumineux intégré à la fusée, de quelques lois physiques et mathématiques (peu, rassurez-vous) et des Dupondt. Vous avez tout ce qu'il faut ? Très bien, nous pouvons partir.

Tout d'abord, larguons Dupont dans l'espace, tandis que Dupond monte dans la fusée⁽¹⁾ ; faites faire demi-tour à la fusée afin qu'elle repasse devant Dupont à une vitesse élevée, mettons 200 000 km/s, et allumons le faisceau quand elle passe devant Dupont. Comparons alors ce que voient nos deux inspecteurs :

• 
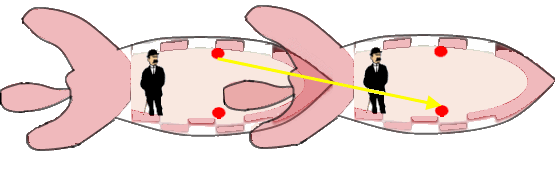
  Ce que voit Dupont : un rayon de lumière diagonalPour Dupont, qui voit la fusée se décaler, la lumière (qui se décale en même temps que la fusée) décrit une ligne droite oblique ;

• 
  Ce que voit Dupond : un rayon de lumière vertical Pour Dupond, la lumière parcourt une ligne droite verticale.

En sachant que la lumière possède une vitesse absolue⁽²⁾, et en utilisant le théorème de Pythagore et la relation \(v=\frac{d}{t}\), on trouve : \(T_{obs}=\frac{T_{fus}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\), avec \(T_{obs}\) le temps de l'observateur extérieur (Dupont), \(T_{fus}\) le temps pour l'observateur en mouvement (Dupond), \(c\) la vitesse de la lumière, et \(v\) la vitesse de la fusée. Plus précisément, en divisant par \(T_{fus}\), on obtient le facteur de dilatation du temps, noté \(\gamma\), également appelé facteur de Lorentz : \(\gamma = \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\)
Ce qui est surprenant dans cette formule, c'est que dès que vous bougez (que vous acquérez une vitesse), vous avancez dans le temps ! Enfin, tout est relatif⁽³⁾ puisqu'à 900 km/h – la vitesse moyenne des avions – \(\gamma\) ne vaut que 1,000 000 000 000 4 et des poussières, c'est-à-dire franchement pas grand-chose⁽⁴⁾… Par contre, \(\gamma\) vaut 2 vers 260 000 km/s, et plus vous vous rapprochez de la vitesse de la lumière, plus la valeur de \(\gamma\) augmente rapidement, jusqu'à tendre vers l'infini ! Ainsi, si vous volez à 299 750 km/s pendant un an⁽⁵⁾ à votre retour, tous vos amis (et les autres) auront pris presque 60 ans !
Alors, qu'est-ce qui nous empêche d'aller dans le temps voir quelle sera la météo des siècles prochains, vous direz-vous ? Eh bien, c'est tout simplement la technologie : rappelez-vous que vous devez arriver à une vitesse énorme, et ça, c'est pour le moment impossible.

Il existe une autre solution dont profitent actuellement tous les satellites terrestres : la gravité. En effet, le temps s'écoule plus lentement lorsque l'on est proche d'un corps massif (e.g. la Terre) que lorsque l'on en est éloigné⁽⁶⁾. Dans ces conditions, une des meilleures machines temporelles « naturelles » reste Sagitarius A*, un trou noir, situé au centre de la Voie Lactée, de quelques millions de fois la masse de notre Soleil. Avec lui, il est sûr que vous pourrez voyager dans le temps, mais vous ne risquez pas d'en ressortir…

Mais puisque vous, fidèles lecteurs d'Omnilogie, n'êtes pas concernés par ce genre de détails si bassement terre à terre, précipitez-vous dans le futur pour lire un prochain omnilogisme, afin de savoir comment rentrer sain et sauf dans notre temps présent.

---

1. ⁽¹⁾ ↑ Pour vous souvenir de qui est qui : Dupond est dans la fusée.
2. ⁽²⁾ ↑ En gros, quelle que soit votre vitesse (même 299 000 km/s), si un rayon de lumière vous dépasse, sa vitesse par rapport à vous sera toujours de 299 792,458 km/s, soit la vitesse de la lumière. On dit que la vitesse de la lumière ne dépend pas du référentiel depuis lequel on l'observe. Surprenant, non ?
3. ⁽³⁾ ↑ Et devinez à qui l'on doit cette découverte ? Einstein, suite à sa théorie de la relativité restreinte !
4. ⁽⁴⁾ ↑ Sauf si vous considérez que voler 100 000 ans pour gagner 1 seconde est significatif !
5. ⁽⁵⁾ ↑ Soit tout de même 99, 99 % de la vitesse de la lumière…
6. ⁽⁶⁾ ↑ Ainsi, tous les satellites « avancent » d'un tiers de milliardième de seconde chaque jour, ce qui peut entraîner de grosses répercussions sur le guidage GPS, où une très grande précision est nécessaire.

Cet article vous a plu ? Courez lire la suite !