La Terre est ronde.

On se dit ainsi que, pour se rendre d'un point \(A\) à un point \(B\), il faut parcourir l'arc de cercle qui nous sépare de lui, sur la courbe terrestre. Je vous propose donc d'effectuer deux calculs : le premier consiste à calculer la distance exacte entre nos deux points, l'autre à calculer l'arc de cercle correspondant, pour savoir à quel point « la ligne droite est la plus courte distance entre deux points ».

Nommons \(\Omega\) notre cercle (ici, une coupe de la sphère terrestre), \(A\) notre point de départ, \(B\) notre point d'arrivée, \(O\) le centre du monde⁽¹⁾ et \(C\) le point du cercle symétrique de \(A\) par rapport à \(O\).

\(AC\) est donc le diamètre du cercle. On peut donc poser une première propriété qui va beaucoup nous aider : tout triangle inscrit dans un cercle est rectangle si les points qui le forment sont deux points formant le diamètre et un troisième point n'importe où sur le cercle. En clair, le triangle \(ABC\) est rectangle en \(B\) car \(AC\) est le diamètre du cercle.

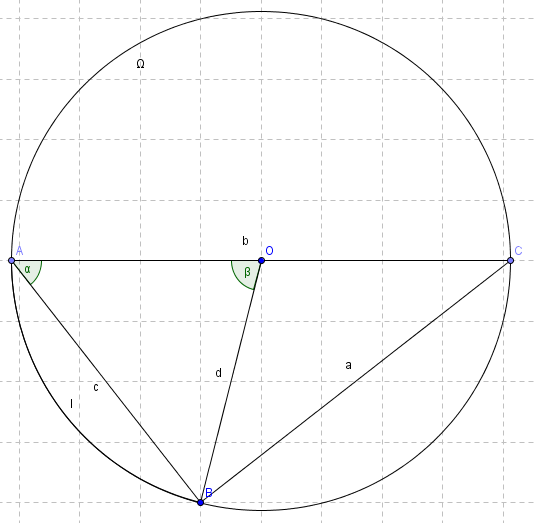
Calculons donc la distance qui nous intéresse, \(AB\), soit \(c\).

On utilise la forme apprise en troisième \(cos \alpha = \frac{c}{b}\) avec \(b\) le diamètre de la Terre pour en déduire \(c = cos \alpha \times b\).

Maintenant, donnons l'expression de la formule de l'arc de cercle. Si on réfléchit en degrés d'angle :

\(l = \frac{\beta \times \pi \times r}{180}\)

On va donc calculer la différence entre la distance réelle entre nos deux points et la distance parcourue (l'arc) :

\(l - c = \frac{\beta \times \pi \times r}{180} - cos \alpha \times b\)

\(r\) est le rayon de la Terre, soit \(\frac{b}{2}\). On factorise donc par \(b\) :

\(l - c = b \times (\frac{\beta}{360} \times \pi - cos \alpha)\)

Nous allons donc donner un encadrement de \(l - c\) pour voir comment cette distance varie. \(l - c \geq 0\) car un arc de cercle est toujours plus grand que le segment qui le compose. \(b > 0\) (c'est le diamètre de la Terre), il n'intervient donc pas dans le calcul. On en déduit donc que :

\(\frac{\beta}{360} \times \pi - cos \alpha \geq 0\)

On a également les paramètres suivants :

\(0 \leq \beta \leq 180\)

\(0 \leq \frac{\beta}{360} \leq \frac{1}{2}\)

\(0 \leq \frac{\beta}{360} \times \pi \leq \frac{\pi}{2}\)

\(0 \leq \alpha \leq 90\)

\(0 \leq cos \alpha \leq 1\)

Ainsi :

\(0 \geq \frac{\beta}{360} \times \pi - cos \alpha \geq \frac{\pi - 2}{2}\)

\(b = r \times 2 = 6371000 \times 2 = 1,2472 \times 10^7 m\)

D'où :

\(0 m \leq b \times (\frac{\beta}{360} \times \pi - cos \alpha) \leq 1,2472 \times 10^7 m\)

On comprend que, plus les deux points sont proches, plus la différence entre la valeur de l'arc et la valeur du segment est petite. Toutefois, pour des points très éloignés, la différence peut aller jusqu'au diamètre ! C'est pour cela qu'il faut privilégier la mesure de l'arc, qui est, elle, plus précise et plus représentative du chemin parcouru⁽²⁾.

La formule pour mesurer l'arc est tout à fait correct. Cependant, des mathématiciens ont trouvé une formule permettant de calculer cette distance à l'aide des longitudes et latitude des deux points. C'est plus pratique que de mesurer un angle… Voici cette formule, ainsi que le schéma correspondant :

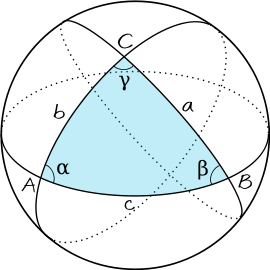
\(c = r \times arccos(sin \phi_{A} sin \phi_{B} + cos \phi_{A} cos \phi_{B} cos (\lambda_{A} - \lambda_{B}))\)

Où \(r\) est le rayon de la Terre, \(\phi_{A}\) et \(\phi_{B}\) les longitudes des points \(A\) et \(B\), \(\lambda_{A}\) et \(\lambda_{B}\) les latitudes des points \(A\) et \(B\).

Bigre ! Quelle formule ! Cependant, comme j'ai à cœur de vous simplifier les choses, voici comment l'on peut arranger la formule, en notant :

\(cos (\Delta \lambda) = cos (\lambda_{A} - \lambda_{B})\)

\(c = r \times arccos(cos(\phi_{A} - \phi_{B}) + cos(\Delta \lambda) (cos \phi_{A} cos \phi_{B} - 1))\)

---

1. ⁽¹⁾ ↑ Que celui qui reconnaît ici une subtile référence à Dali lève la main ! Cet admirable peintre fou considérait Perpignan comme le centre du monde. Il avait tort. Car le vrai centre, c'est \(O\). Et toc.
2. ⁽²⁾ ↑ Car on n'a pas encore inventé les foreuses qui nous permettraient de traverser la croûte terrestre de part en part pour joindre une autre ville.