Quelle est la différence entre un tuyau d'arrosage et un turboréacteur ?

Afin de répondre à cette question⁽¹⁾, intéressons-nous tout d'abord à un phénomène que quiconque ayant eu un jour un tuyau d'arrosage entre les mains a pu constater : quand on pince l'ouverture⁽²⁾, l'eau va plus loin.

L'explication physique de ceci⁽³⁾ tient à la conservation du débit masse. Dans cette formule, \(D_m\) est le débit masse, \(\rho\) la masse volumique du fluide considéré, \(v\) sa vitesse, et \(S\) la surface de sortie :

\(D_m=\rho \times v \times S = constante\)

On voit ici qu'en considérant la masse volumique \(\rho\) constante pour le fluide, une diminution de la surface de sortie entraîne une augmentation de la vitesse de sortie⁽⁴⁾, et donc de la distance parcourue par le jet⁽⁵⁾.

À ce moment de l'article, le lecteur attentif⁽⁶⁾ fait remarquer à l'auteur : « Et donc, ce turboréacteur, quand arrive-t-il ? »
Et l'auteur de répliquer au lecteur⁽⁷⁾ : « Eh bien, juste maintenant ! »

Voici donc un turboréacteur (de fusée) :

Et le lecteur appliqué⁽⁶⁾ de pointer : « Qu'est-ce que c'est que ces sornettes, on voit bien que la surface de sortie augmente pour ce turboréacteur ! »

Et il aura bien raison. En effet, pour ce turboréacteur comme pour tous les turboréacteurs, qu'ils soient de fusée ou d'avions de chasse (la plupart, en tous cas), se terminent en cône ouverts sur l'extérieur. Selon notre conservation du débit masse, cela devrait entraîner une diminution de la vitesse de sortie du fluide (en l'occurrence, du gaz), ce qui diminuerait de fait la poussée engendrée par l'engin. Cependant, souvenez-vous, nous avions alors considéré la masse volumique comme constante, et si cette approximation est tout à fait envisageable pour un tuyau d'arrosage, dans le cas d'un turboréacteur, avec des vitesses supérieures à la vitesse du son, cela n'est plus du tout correct !

En fait, pour un fluide supersonique, la relation entre surface et vitesse de sortie est inversée : une augmentation de surface entraîne une augmentation de vitesse ! Ouf, nos fusées voleront bien.

Voilà pour la description physique. À présent, pour ceux qui le désirent, tentons une approche plus calculatoire du phénomène⁽⁸⁾.

Après quelques manipulations mathématiques⁽⁹⁾, on peut obtenir la formule dite de Rankine-Hugoniot, qui décrit la variation de la vitesse de sortie d'un fluide en fonction de la surface de sortie, et ce sans prendre aucun autre paramètre en compte (ce qui évite de devoir faire des approximations sur la masse volumique, par exemple). Voici donc la formule avec \(dS\) la variation de la surface de sortie, \(dv\) la variation de la vitesse de sortie, et M le nombre de Mach, \(M=\frac{vitesse du fluide}{vitesse du son}\) :

\(\frac{dS}{S}=(M^2-1)\frac{dv}{v}\)

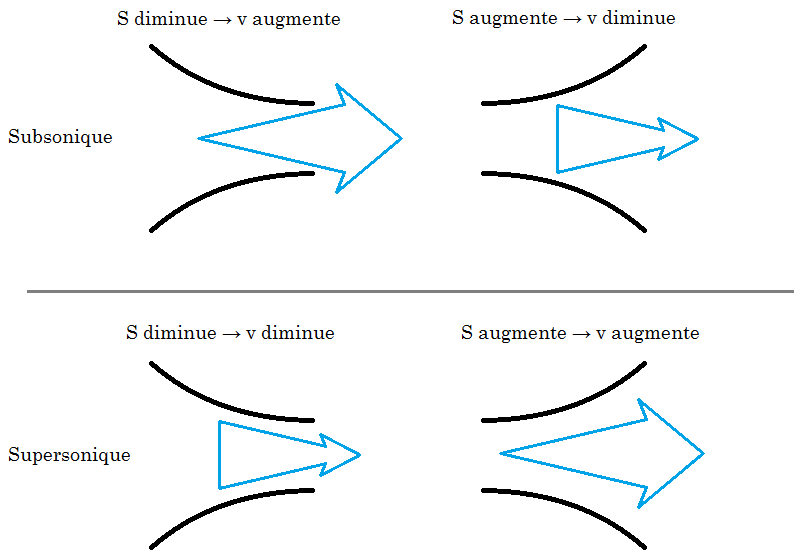
Dans le cas subsonique, \(M < 1\), \((M^2 - 1)\) est négatif, et la variation de la surface de sortie entraîne une variation inverse de la vitesse de sortie.
Dans le cas supersonique, en revanche, \(M > 1\), et donc \((M^2 - 1)\) est positif, la vitesse de sortie varie comme la surface de sortie ; nous retrouvons bien les résultats précédents !

C'est ce double phénomène qui amène les constructeurs d'avions à façonner les réacteurs en forme de « sablier penché ». La première partie, où la surface se réduit progressivement, accélère les gaz jusqu'à la vitesse du son. La seconde partie, visible de l'extérieur et où la surface augmente, accélère ensuite ces gaz au-delà de la vitesse du son (mais ce n'est pas le seul phénomène utilisé, bien entendu) : voilà notre avion supersonique !

---

1. ⁽¹⁾ ↑ En laissant de côté les réponses les plus évidentes, sans quoi il y en a pour la journée…
2. ⁽²⁾ ↑ On considère ici un tuyau d'arrosage sans embout.
3. ⁽³⁾ ↑ On entre alors dans le domaine de la mécanique des fluides.
4. ⁽⁴⁾ ↑ Et vice-versa, une augmentation de la surface de sortie entraîne une diminution de la vitesse de sortie du fluide.
5. ⁽⁵⁾ ↑ Et voilà le premier quidam passant par là tout trempé alors qu'il se croyait hors d'atteinte.
6. ⁽⁶⁾ ↑ Comme tous les lecteurs d'Omnilogie !
7. ⁽⁷⁾ ↑ Tout en le remerciant de son intervention bien minutée…
8. ⁽⁸⁾ ↑ Avis à ceux que les équations rebutent : sauvez-vous !
9. ⁽⁹⁾ ↑ Relatées ici.