Les probabilités, ce n'est pas intuitif. Ce constat terrible me hante depuis des années. Comme le montre le problème de Monty hall, nous avons du mal à sentir des résultats pourtant assez simples. Le problème qui va nous occuper aujourd'hui est un grand classique de la probabilité. Moins connu que le problème sus-cité, la situation se présente néanmoins plus souvent car il s'agit de maladie et de dépistage.

Imaginez qu'une nouvelle maladie terrible apparaisse : la cancerebolaviaire qui touche spontanément une personne sur 100 000 et qui tue à tous les coups. Heureusement, les chercheurs parviennent assez vite à trouver un test de dépistage de cette maladie. Le test est suffisamment simple pour être effectué en pharmacie et reste tout de même très efficace (99,9 % de taux de bonne réponse, c'est du sérieux). Par curiosité, vous faites le test et, c'est terrible, il revient positif. Est-ce que vous rédigez vos dernières volontés ?

Non, non et non ! À combien estimez-vous vos chance de mourir ? Presque 100% ? Vous n'avez pas lu l'introduction ma parole et vous êtes loin du compte. 10% ? Vous sortez ça de votre chapeau ? En réalité, vous avez moins d'une chance sur cent d'être vraiment malade, 1%, rien que ça. Le test sert simplement à justifier des examens complémentaires(1).

Vous ne me croyez pas ? Regardez, prenez 100 millions de personnes. Vous avez 1000 malades presque tous repérés par le test. Mais parmi la masse de personnes saines, le test fait tout de même presque 100 000 de faux positifs (0,1 % d'erreur, rappelez-vous). Vos chances d'être réellement malade sachant que le test est positif ne sont donc qu'environ de 1000 (nombre de malades testés positif) sur 101 000 (nombre de tests positifs) soit 1 petit pourcent(2).

Comment en arrive-t-on à une situation pareille ? C'est à cause de la différence d'ordre de grandeur entre le défaut du test (0,1%) et la rareté de la maladie (0,001%) soit deux ordres de grandeur. C'est à peu près la limite. Si le test était encore 10 fois plus mauvais (1% d'erreur), vous n'auriez que 9 chances sur 100 000 d'être vraiment malade soit quasiment vos chances a priori d'être malade sans test (1 sur 100 000). Autant dire qu'on ne progresse pas beaucoup… Mais pour bien se rendre compte de la relation entre la qualité du test et la rareté de la maladie, jetez-donc un œil au graphique suivant, les valeurs sont plutôt simples et surtout symétriques :

Évolution des chances d'être malade sachant que le test est positif en fonction de la qualité du test pour une fréquence de maladie de 1 pour 100 000.

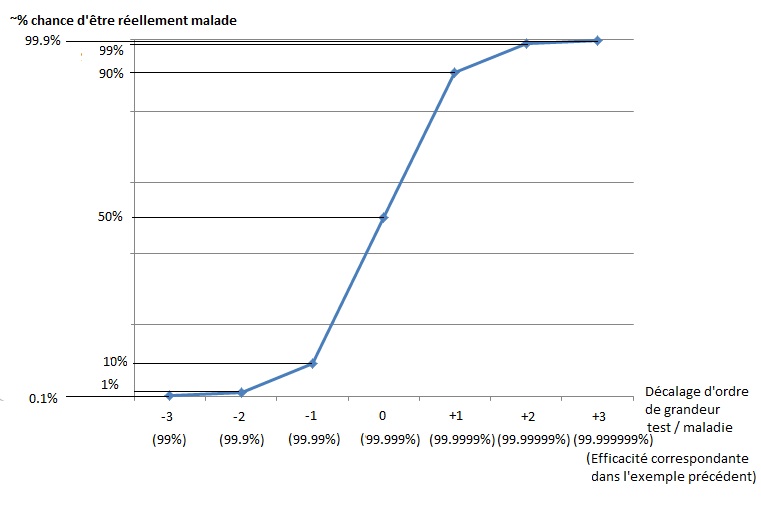
En pratique, la situation est légèrement différente. On effectue un test de dépistage seulement s'il y a des raisons de suspecter une contamination. On élimine donc une bonne proportion des individus sains dans les tests, cela revient à augmenter artificiellement la fréquence de la maladie, ce qui améliore le résultat du test. C'est pourquoi il vaut mieux suivre les conseils de son médecin avant de faire un dépistage. En effet, chaque hypocondriaque plombe les statistiques et donc la crédibilité du test.

  1. (1) ↑ Tout est une question de dosage entre le prix (ou le coût humain) du test de dépistage, celui des examens complémentaires et celui du traitement, qui normalement sont croissants.
  2. (2) ↑ Le calcul réel est de 999 (nombre de malades détectés avec succès) / (99 999 + 999) (nombre de tests positifs). Pour comprendre le calcul, c'est une application de la formule de Bayes.