Les fractales sont ces objets fascinants qui se contiennent eux-mêmes, en présentant toujours un même nombre de détails quelle que soit la profondeur à laquelle on s'enfonce en eux. Prêt pour un voyage dans l'infini ?

Les fractales sont partout autour de nous. Ah bon ? Eh oui, on en trouve même au marché, à la bonne saison. Je veux bien sûr parler des choux de Romanesco, ces légumes qui s'apparentent au brocoli :

Les puristes me diront que ce n'est pas une vraie fractale, puisque le fruit ne se répète pas à l'infini. C'est vrai, la Nature ne pourrait pas maintenir tel quel un objet si fragile et si finement sculpté. Et puis, on finirait par arriver à l'échelle de l'atome à un moment ou à un autre, et ça s'arrêterait là.
En passant, les fougères sont elles aussi un modèle de fractales :

Et les « vraies » fractales alors ? Et bien, ce sont des objets mathématiques, qui peuvent être très simples, mais aussi très complexes pour certains. En général, une fractale est plutôt construite sur un principe simple, sinon, ça devient infernal.
Voici quelques exemples :

• Le triangle de Sierpinski : c'est un triangle qui contient des triangles, qui contiennent des triangles…

  

• L'éponge de Menger : c'est un petit peu le même principe, mais en cubique.
  Une photo de la dame :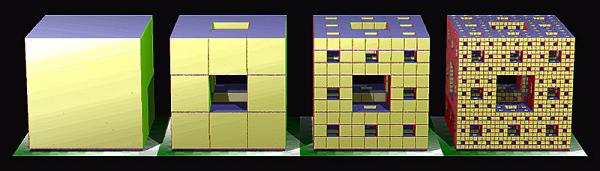

  

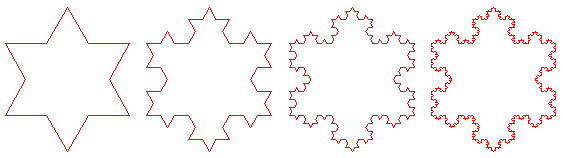
• La courbe de Von Koch : on trace un triangle équilatéral. On découpe chacun de ses côtés en trois tiers. On dessine un triangle équilatéral sur chaque tiers « du milieu », et on efface ce dernier. On répète l'opération indéfiniment, et voilà ce qu'on obtient :

  

• Enfin, l'ensemble de Mandelbrot : Benoît Mandelbrot vaudrait bien un article à lui tout seul, étant le père du terme « fractale »⁽¹⁾, et tant il a influencé le monde des mathématiques dans ce domaine.
  Voilà une image de l'ensemble seul :

  

  Seulement, on s'est rendu compte qu'il devenait bien plus intéressant de colorer les parties n'appartenant pas à l'ensemble en fonction de leur proximité. (C'est ici une proximité mathématique et non géométrique, ne vous attendez pas à un joli dégradé). Voilà ce qu'on obtient :

  
  Et où qu'on zoome sur l'image, on pourra toujours retrouver le même motif :

  
  Enfin, une dernière image pour terminer :

  

Et voilà, fin du petit tour d'horizon. Les fractales sont pour moi des objets fascinants parce qu'on y trouve tout un monde, en particulier dans les fractales assez complexes comme celle de Mandelbrot. On y trouve même à l'intérieur une autre fractale, l'ensemble de Julia⁽²⁾. Et si vous trouvez un ensemble de Julia dans celui de Mandelbrot, et que vous zoomez à l'intérieur, vous pourrez retomber à nouveau sur un ensemble de Mandelbrot. Quand la petite bête mange la grosse…

---

1. ⁽¹⁾ ↑ Qu'il a formé à partir du latin fractus, qui signifie brisé.
2. ⁽²⁾ ↑ Le premier qui demande « Et où est-ce qu'il est ? » a gagné un petit rappel : c'est partout. Dans une fractale, rien n'est unique, tout existe à l'infini, et se trouve partout. Vous aurez toujours une infinité de détails où que vous alliez.