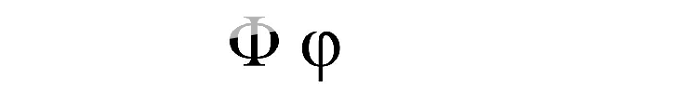
Les maths de la nature
Saviez-vous qu'on pouvait trouver des mathématiques dans la nature ?
Abstraites, compliquées, servent peu dans la vie de tous les jours, voilà des caractéristiques que beaucoup de gens peuvent attribuer aux maths. Or un certain nombre de propriétés mathématiques se retrouvent dans la nature.


Fractale de Mandelbrot.
Une fractale est une figure mathématique qui se répète à l'infini en se reproduisant sur les côtés des répétitions précédentes. Et si on observe le brocoli à la loupe on peut voir que les petits grains ont sur leur surface de plus petits grains, eux-même ayant de plus petits grains sur leur surface et ainsi se suite.
Ces objets ont été créés par Benoît Mandelbrot, un mathématicien polonais, dans le but d'expliquer les formes présentes dans la nature dont la géométrie était trop irrégulière pour être expliquée par la géométrie classique.
Le brocoli n'est donc pas le seul exemple, on trouve aussi le choux-fleur.

Fleur dont les pétales forment un pentacle.
Mais on peut aussi trouver dans la nature d'autres objets mathématiques comme le nombre d'or défini par : \(\phi\)=\(\frac{1+\sqrt{5}}{2}\)
En coupant une pomme en deux on voit que les pépins dessinent un pentacle. Des mathématiciens ont observé dans la disposition des pétales des fleurs ou encore dans la façon dont s'enroulent les écailles d'une pomme de pin ou d'un ananas l'apparition du nombre \(\phi\). D'ailleurs, certaines fleurs ont cinq pétales répartis uniformément. En outre il est présent chez l'homme, le nombril divisant le corps suivant \(\phi\)
Enfin, comme dernier exemple, je vous présente la suite de Fibonacci définie par :
\(U_{n+2}=U_{n+1}+U_{n}\) avec \(U_{0}=1\) et \(U_{1}=1\)
Cette suite « s » retrouve par exemple dans les spirales du tournesol et d'autres végétaux, d'ailleurs celles-ci sont disposées selon l'angle d'or : \(\alpha=\frac{360}{1+\phi}\)