Analysons les deux propos suivants :

A : Socrate est un homme, les hommes sont mortels, donc Socrate est mortel.

B : Toutes les Ferrari sont rouges, ma voiture est rouge, donc ma voiture est une Ferrari.

Quelle est la différence entre ces deux propos ? Le premier nous semble pertinent. Le second, pourtant, est particulièrement étrange. Le raisonnement logique proposé semble incorrect. Oui, mais si ma voiture est effectivement une Ferrari ? Cela ne change pas la nature de l'erreur qui nous embête. Le cheminement est faux… pourtant, sa conclusion est vraie.

Alors peut-être sont-ce les prémisses de ce syllogisme, les deux propositions initiales, qui se révèlent incorrectes ? Examinons-les.

• Toutes les Ferrari sont rouges : hormis la généralisation un peu grossière, on peut, pour cet exemple, considérer cette prémisse comme correcte.
• Ma voiture est rouge : c'est indéniable.

Mais qu'est-ce qui ne va pas ? Les prémisses sont bonnes, la conclusion aussi. Il ne reste qu'une seule chose qui puisse clocher : le lien logique qui permet de passer des unes à l'autre : ce n'est pas parce que ma voiture est rouge que c'est une Ferrari ! En effet, parmi toutes les voitures de couleur rouge, certaines sont des Ferrari et d'autres n'en sont pas.

Avec cet exemple, on voit bien que dans la réalité, prémisses et conclusion sont vraies, et pourtant le raisonnement est faux : il faut donc distinguer la validité d'un raisonnement de sa véracité ou vérité. Un raisonnement est valide si les connecteurs logiques et plus généralement tout le vocabulaire logique sont employés correctement. Il est vrai si prémisses et conclusion sont vraies dans la nature⁽¹⁾.

Dans l'absolu, il existe un raisonnement valide et vrai, un raisonnement valide mais faux, un raisonnement invalide mais vrai, un raisonnement invalide et faux.

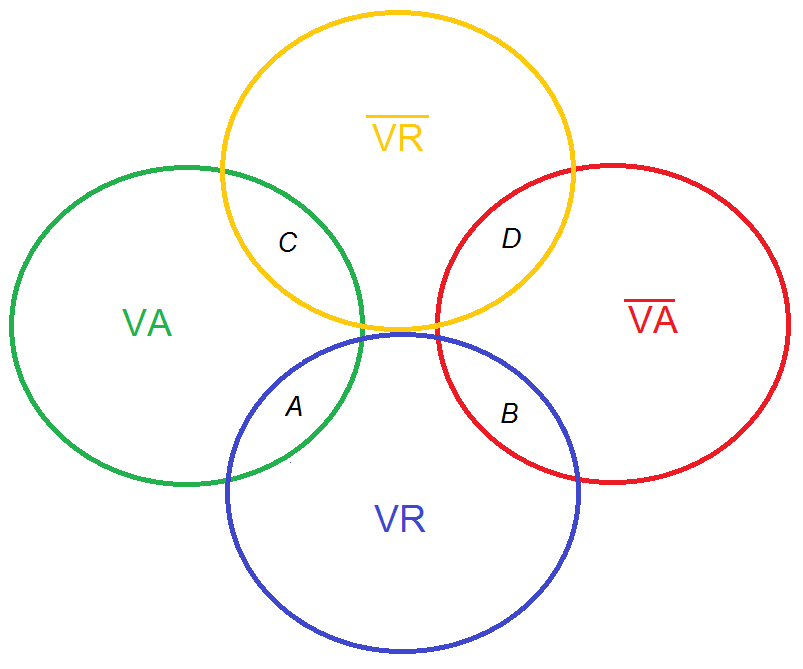
Raisonnons par ensembles. Notons \(VA\) l'ensemble des raisonnements valides, \(\overline{VA}\) les invalides ; \(VR\) les raisonnements vrais, \(\overline{VR}\) les raisonnements faux. Je vous propose de trouver un exemple de chaque cas mentionné au-dessus. Nous savons que \(A\) est vrai et valide, donc \(A\) appartient à l'ensemble des valides et des vrais, et cela se note :

\(A \in VA \cap VR\)

Le symbole \(\in\) exprime l'appartenance d'un objet unique à un ensemble. Quant à \(\cap\), il s'agit du symbole d'intersection de deux ensembles.

Quant à \(B\), le raisonnement est vrai mais invalide :

\(B \in \overline{VA} \cap VR\)

Analysons de même les propositions suivantes :

C : Plus il y a de gruyère, plus il y a de trous. Plus il y a de trous, moins il y a de gruyère. Donc plus il y a de gruyère, moins il y a de gruyère.

Ce paradoxe assez célèbre montre bien les problèmes causés par le langage en logique. La conclusion est fausse, le raisonnement est donc faux ; cependant, le raisonnement est valide. Nous pouvons classer \(C\) :

\(C \in \overline{VR} \cap VA\)

Il est toujours plus difficile de trouver un raisonnement qui satisfait la condition de véracité et pas celle de validité ou inversement. En revanche, trouver un raisonnement valide et vrai ou invalide et faux, c'est facile. La preuve, voici le dernier :

D : Les tableaux à feutre sont blancs, certains chiens sont blancs, donc certains chiens sont des tableaux à feutre.

Cet énoncé est bien sûr faux et invalide :

\(D \in \overline{VR} \cap \overline{VA}\)

Vous pouvez visualiser chacun de ces raisonnements sous forme de tableau ou sous forme de schéma :

Classement des quatre énoncés

	\(VA\)	\(\overline{VA}\)
\(VR\)	A	B
\(\overline{VR}\)	C	D

⁽²⁾

---

1. ⁽¹⁾ ↑ Il faut que les trois propositions soient correctes simultanément. Il suffit qu'un seul des trois morceaux soit faux pour que le raisonnement le soit aussi
2. ⁽²⁾ ↑ Vous remarquerez que les ensembles opposés, \(VA\) et \(\overline{VA}\), n'ont aucune intersection commune. Cela paraît logique, un objet ne peut appartenir simultanément à deux ensembles disjoints (qui n'ont aucun élément commun). C'est le principe essentiel de non-contradiction logique.