Le monde des probabilités est vraiment étrange. Un univers où seuls les plus hardis osent s'y risquer. Si tu veux continuer à lire ceci, prépare-toi. Ton rythme cardiaque augmente ? Ta sudation passe à la vitesse supérieure ? Aurais-tu peur, par hasard ? Probablement.
Le problème, appelé problème de Monty Hall, est donc le suivant⁽¹⁾.

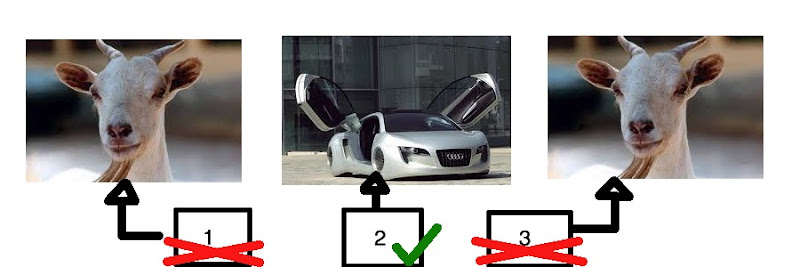
Vous voici à l'antenne, dans un jeu télévisé, et vous avez le choix entre trois boîtes. Deux contiennent une chèvre et l'autre une magnifique voiture⁽²⁾.

Le présentateur, M. Tchiteur, vous demande de choisir une boîte. Vous choisissez la première, il y a donc une chance sur trois de prendre la voiture. Maintenant, histoire de faire monter le suspense, le présentateur montre le contenu d'une boîte, celui de la troisième, et soulagement, c'est une chèvre.

À ce moment là, M. Tchiteur vous propose de changer votre choix. Dès lors, que faire ? Changer ou conserver son numéro, sachant qu'apparemment, vous avez une chance sur deux de gagner la voiture. Logiquement, changer ou pas reviendrait toujours au même. C'est ici que les méninges vont exploser.
Posons le problème de façon calme et précise.

Au départ, chaque boîte a une chance sur trois de contenir la voiture : vous avez donc 33 % de chance de désigner la bonne boîte dès le début et 66 % de vous tromper.
Cependant, on pourrait formuler différemment les affirmations ci-dessus de façon à ce qu'elles éclairent la résolution du problème. Il y a deux chance sur trois que la voiture se retrouve dans les autres boîtes⁽³⁾. Le fait de dévoiler le contenu (la chèvre) de la troisième ne change en rien cette phrase. Il ne reste alors que deux boîtes inconnues et il y a toujours 66 % de chance que la voiture soit dans la deuxième boîte.

Résumons : la voiture a 66 % de chance de se trouver ailleurs que dans la première boîte, et on sait que dans la troisième, il y a une chèvre. On sait aussi que s'il faut changer son choix, seule la deuxième boîte peut contenir la voiture. Il y a donc 66 % de chance que la voiture se trouve dans cette boîte-ci.
Il faut donc changer son choix initial pour avoir plus de chance de remporter le gros lot⁽⁴⁾.

---

1. ⁽¹⁾ ↑ Je le tiens de mes cours de fac et je remercie au passage mon excellent prof de proba.
2. ⁽²⁾ ↑ Les chèvres et la voiture sont dispersées au hasard dans les boîtes.
3. ⁽³⁾ ↑ Les boîtes deux et trois dans notre cas.
4. ⁽⁴⁾ ↑ Il existe une méthode de résolution par le théorème de Bayes, mais cette approche n'est pas compréhensible par tous à cause d'un usage poussé de l'outil mathématique. Cependant, les plus coriaces peuvent se rendre ici pour se mesurer à cette méthode.