Trouer carré
Comment utiliser la géométrie pour faire des trous carrés ?
Cet article fait partie de la « semaine de l'absurde » sur omnilogie. Chaque jour, un article répondant à une question déterminée au hasard par les membres participants.
Qui ne s'est jamais un jour dit : « mince, mais comment vais-je faire pour faire un trou carré ? »
Personne ?
Ah, tant pis…
Plus sérieusement, il est vrai qu'un trou carré dans un mur ne présenterait pas beaucoup plus d'avantages qu'un bon vieux trou rond pour y accrocher quelque chose. D'autant que ledit trou rond est bien plus facile à faire, et pour cause : le plus simple et rapide pour faire un trou, c'est encore de faire tourner rapidement un foret(1), ce qui permet à la fois de trouer et pénétrer le matériau à percer, et également d'évacuer les débris.
Et a priori, quand on fait tourner quelque chose, ça fait un rond. Pourquoi, d'ailleurs ? Eh bien tout simplement parce qu'un rond (ou pour être plus rigoureux, un cercle) a comme propriété d'avoir tous les points le composant à égale distance de son centre. Donc, si on fait tourner quelque chose autour d'un centre (ou pour être plus rigoureux, un axe), chaque point de notre « quelque chose » décrira un cercle.
Ce qui permet donc d'avoir des jolis trous bien ronds. Mais au final, un trou rond n'est pas toujours le plus pratique : ce qu'on met dedans est susceptible de tourner, et donc d'éroder les bords du trou, et donc l'agrandir. Un trou carré peut donc bel et bien parfois être utile. Seulement voilà, un carré n'est pas rond(2), en conséquence de quoi ce n'est pas si simple d'en trouer un…
C'est là que le triangle de Reuleaux(3) entre en scène !
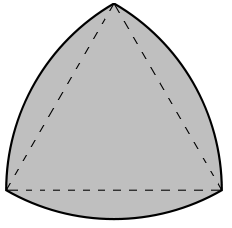
Le triangle de Reuleaux, qui n'est pas un triangle, a cependant une propriété très intéressante : tous ses « côtés » ont la même longueur. On peut en construire un très simplement : à partir d'un triangle équilatéral, on trace trois cercles avec un côté du triangle pour rayon, et pour centres chacun des sommets du triangle :
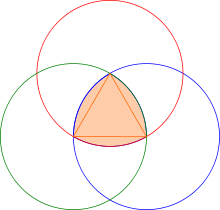
En conséquence, puisque ce sont tous des rayons de cercles de même taille, toutes les « hauteurs » d'un triangle de Reuleaux ont également la même longueur :
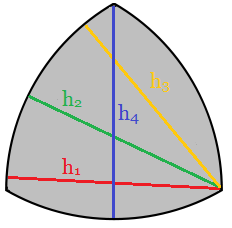
Bon c'est bien beau toutes ces figures, mais je ne vois pas tellement en quoi c'est lié aux trous carrés !
On y arrive ! Déjà, notons que, de par ses propriétés, si on fait rouler un triangle de Reuleaux sur une surface plane, sa hauteur restera constante, comme pour un cercle :
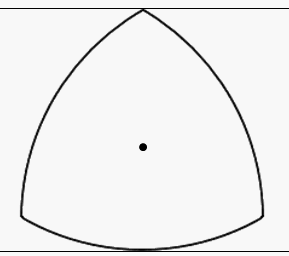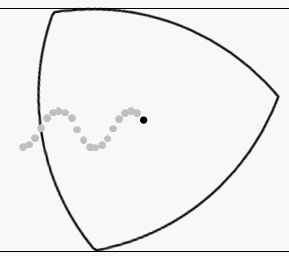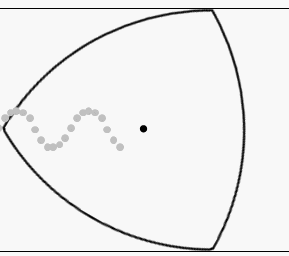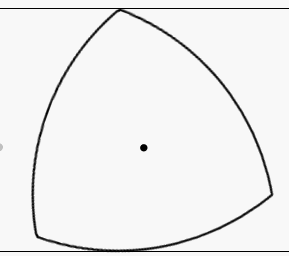
Notez toutefois que, contrairement à un cercle, le centre du triangle de Reuleaux ne reste pas, lui, à la même hauteur.
À partir de là, on y est presque ! Plutôt que de le faire rouler dans une direction, si on essayait de le garder au même endroit ? Puisqu'on peut le faire tenir entre deux barres horizontales de hauteur constante en bougeant son centre de haut en bas, on doit bien pouvoir le faire tenir entre deux barres verticales à distance constante en bougeant son centre de droite à gauche (vu la symétrie du triangle de Reuleaux). Et si on place deux limites horizontales et deux barres verticales, on obtient… Un carré !
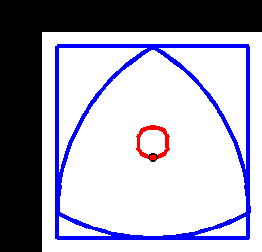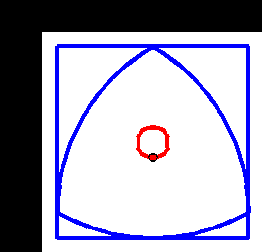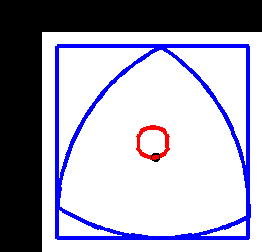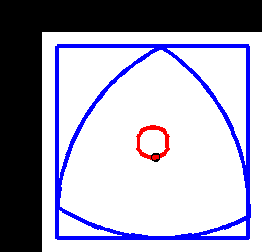
Et le centre du triangle ayant un mouvement horizontal et vertical, il décrit un cercle, tournant en sens inverse du triangle.
Alors en effet, ce n'est pas un carré parfait, les sommets ne sont pas totalement délimités par la rotation du triangle. Mais c'est déjà mieux que rien !
Il n'y a plus qu'à installer un petit coude sur une perceuse (pour obtenir le mouvement en cercle du centre du triangle) et à évider un peu le triangle pour lui donner des « dents » (pour évacuer les déchets), et le trou est joué(4) !
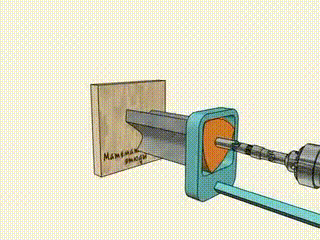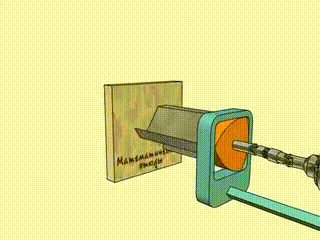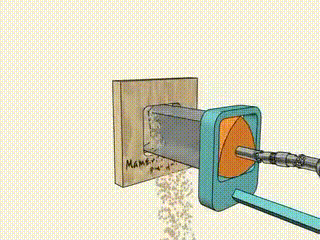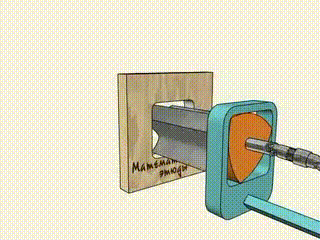
… Et nous passerons sous silence le fait qu'il est de nos jours plus simple de faire des trous carrés grâce à une découpe laser, ou même un jet d'eau sous pression.