Petite question, comme ça : à votre avis, qu'est-ce qui est le plus grand entre le Groenland et l'Australie ? Attention, interdiction de tricher en regardant Google ou Wikipédia. Cela dit, je suis gentil et je vous donne une capture de Google Maps, avec le Groenland et l'Australie d'indiqués.

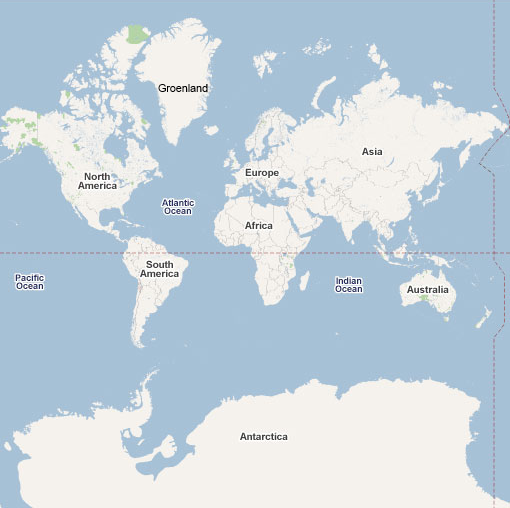
Alors, verdict ? Bon, si je vous ai posé la question, vous vous doutez bien qu'il y a un piège. En effet, alors que le Groenland semble être bien plus vaste que l'Australie, il n'en est rien : en réalité, le Groenland est trois fois plus petit que l'Australie⁽¹⁾ ! Cette « illusion » est due au planisphère que nous utilisons pourtant tous, qui utilise ce que l'on appelle la projection de Mercator. Mais tout d'abord, un peu de maths⁽²⁾ pour se remettre dans le contexte.

Comme vous le savez, notre Terre est ronde. Or, il est mathématiquement impossible de représenter une sphère sur une carte plane sans créer de déformations d'angles ou de surfaces⁽³⁾. Ainsi, tout planisphère comporte des déformations. En l'occurrence, les planisphères qui reposent sur la projection de Mercator sont très étirés au niveau des pôles, parce que la projection de Mercator place lesdits pôles à l'infini⁽⁴⁾ sur la carte. Pour cette raison, le Groenland, très proche du pôle Nord, est énormément étiré ; ce qui n'est pas le cas de l'Australie, relativement proche de l'Équateur.

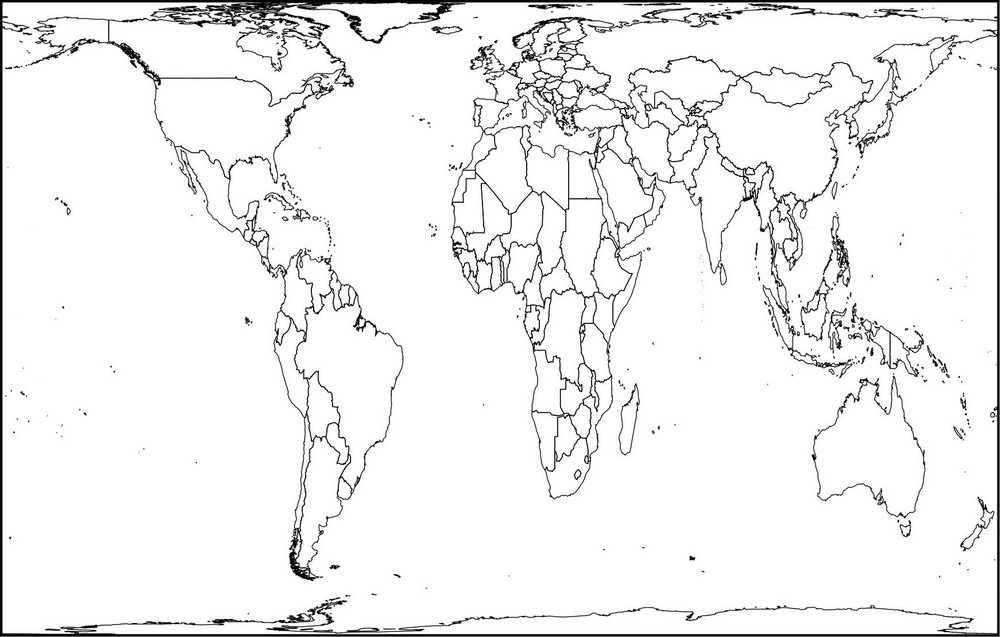
Cela dit, d'autres projections existent, chacune ayant ses avantages et ses défauts, aucune n'étant parfaite⁽⁵⁾. Citons par exemple la projection de Peters, qui conserve les superficies, mais qui perd la fidélité des formes :

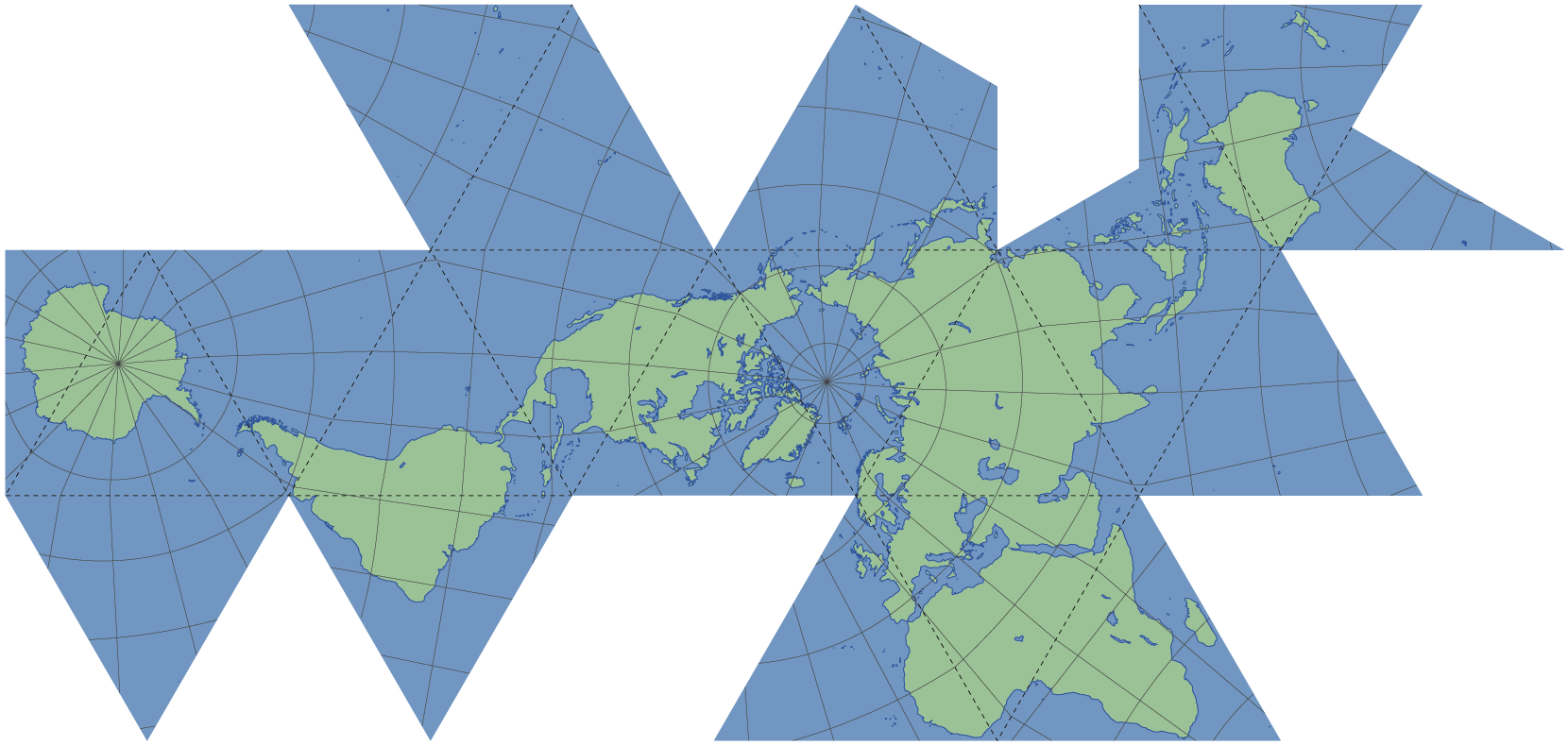
Il y en a bien d'autres, dont certaines pas toujours très carrées, comme par exemple la projection de Fuller ⁽⁶⁾ :

Enfin, avant de nous quitter, voici un site qui vous permet de vous rendre compte de la taille réelle de chaque pays. Par exemple, saviez-vous que l'Afrique était plus grande que l'Amérique du Nord, l'Amérique Centrale et le Groenland réunis, et qu'il restait encore assez de place pour y mettre plusieurs fois la France ? Non ? Eh bien maintenant, vous savez.

---

1. ⁽¹⁾ ↑ C'est bon, vous pouvez utiliser Google. Résultats : Groenland, 2 166 086 km² ; Australie, 7 692 024 km².
2. ⁽²⁾ ↑ Très peu, je vous rassure ! Ne partez pas en courant, de toute manière j'ai déjà verrouillé toutes les issues.
3. ⁽³⁾ ↑ Pour vous en convaincre, essayez d'enrouler une feuille de papier autour d'une surface ronde, comme par exemple un pamplemousse. Vous allez voir que vous serez obligés de faire des plis, avec des bouts de papier qui ne seront pas collés au pamplemousse. Du coup, les mathématiciens « déforment » la Terre pour qu'elle colle parfaitement au papier, ce qui donne ce que l'on appelle une projection.
4. ⁽⁴⁾ ↑ D'ailleurs, c'est pour cela que l'Antarctique apparaît aussi grand sur cette carte : comme le pôle Sud se trouve en Antarctique, cela veut dire que l'Antarctique s'étend à l'infini sur ce genre de cartes – mais comme l'infini c'est loin, on préfère arrêter la carte avant.
5. ⁽⁵⁾ ↑ L'avantage de la projection de Mercator, par exemple, c'est qu'elle conserve (localement) les angles. Par exemple, les méridiens et les parallèles sont bien perpendiculaires, ce qui n'est pas toujours le cas sur les cartes utilisant d'autres projections.
6. ⁽⁶⁾ ↑ Cette projection ne conserve ni les angles ni les superficies, mais les déformations sont bien moindres que sur les deux cartes précédentes (notez d'ailleurs la taille du Groenland et de l'Australie sur cette carte). Quoi qu'il en soit, d'après Wikipédia, la meilleure de toutes les projections reste actuellement celle de Winkel-Tripel.