J'évoquais l'énigme du garçon de café comme une petite introduction au sujet du miroir. Mais je me suis dit que sa résolution n'était pas forcément évidente. Je donne ici une vision que j'espère pédagogique du problème.

Pour commencer, voici un rappel du sujet :

Trois amis refont le monde à une terrasse de café à Paris. Ils ont bu chacun un diabolo menthe et l'addition s'élève donc à 30 euros. Chacun des trois comparses paie dûment sa part de 10 euros au garçon. Mais le patron, de bonne humeur, accorde une remise de 5 euros sur l'addition, 5 euros qu'il rend donc au garçon. La garçon, décide de ne rendre qu'un euro à chacun des clients et conserve donc deux euros pour lui. La question est la suivante : chacun des clients a payé 10 euros moins l'euro qu'il a récupéré. Cela fait donc 27 euros en tout, auxquels on peut ajouter les deux euros que le garçon a conservé pour compléter la note initiale de 30 euros. Raté, cela fait 29 ! Que s'est-il passé ?

La réponse, comme vous vous en doutez, est qu'on somme des montants qui ne devraient pas se trouver ensemble. Cela se comprend mieux en changeant un peu les sommes. Imaginons que le garçon soit un véritable rat et qu'il ne rende qu'un seul centime à l'ensemble des clients. Les clients auraient payé 29,99€ auxquels on chercherait à ajouter le pourboire du garçon de 4,99€. Cette fois-ci il ne manquerait plus un euro, on dépasserait carrément de 4,98€ la note initiale. Comme les banques n'utilisent pas cette méthode pour la création monétaire, c'est qu'il y a anguille sous roche.

En effet, il faudrait plutôt raisonner ainsi : les client ont payé effectivement 27 euros auxquels on ajoute les 3 euros qui leur ont été rendus pour former la note initiale de 30 euros⁽¹⁾. Une méthode sûre pour éviter de se tromper est de visualiser les flux monétaires du problème. Pour comprendre le schéma, une flèche correspond à un transfert d'argent. Pour un portefeuille donné, la somme est négative si la flèche sort et positive si le flèche entre dans le portefeuille. On dira donc que l'on « paye » une somme positive si une flèche de ce montant « sort ». Cela correspond donc à un montant négatif pour le portefeuille. C'est un simple bilan, facile !

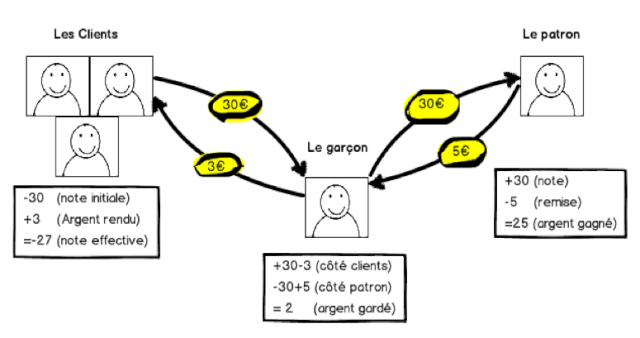
La somme des flux entrants et sortants des clients donne la note effectivement payée (-30 + 3 = -27 euros pour le compte clients). La même chose concernant le patron donne l'argent qu'il a reçu (30 – 5 = +25 euros pour le compte du patron). La somme des flux sur le garçon donne sa balance (+2 euros de pourboire)⁽²⁾. Vouloir, comme dans l'énigme, sommer l'argent payé par les clients et l'argent gardé par le garçon n'a aucun sens. En effet, on somme l'ensemble des flux du garçon (+2 euros) exception faite du flux client-vers-garçon (27€) qu'on décide magiquement de sommer une seconde fois (+2 +27 euros), pour obtenir un nombre qui n'a donc qu'une signification magique⁽³⁾.

Afin d'éviter de faire des bêtises, il faut bien garder à l'esprit la définition des sommes qu'on cherche à exprimer. Ces définitions permettent d'en déduire des moyens alternatifs pour les calculer.

Ainsi la « somme effectivement payée par les clients » correspond à la somme des flux par rapport aux clients (-30+3 = -27, leur portefeuille a bien été retranché de 27 euros).

La « somme conservée par le garçon » est l'ensemble des flux sur le garçon (côté client (+30-3) + côté patron (-30+5) = +2).

Enfin, la « note initiale » ou « note avant remise », celle dont on cherche une méthode alternative de calcul dans l'énigme, correspond du point de vue du client à l'inverse de leur flux initial (ce qu'ils ont payé avant la remise, soit 30 euros). Or on a parfaitement le droit de faire un calcul alternatif en disant qu'un flux en particulier (-30 euros) est égal à la somme de tous les flux (-30 + 3 = -27) retranché de tous les autres flux (- +3)⁽⁴⁾. On retrouve alors le calcul correct annoncé plus haut : la note initiale vaut (-27 -3) = -30 euros, les clients auraient dû payer 30 euros et cela correspond aux 27 euros payés additionnés aux 3 euros rendus).

J'espère ne pas avoir perdu tout le monde avec cette démonstration pompeuse. Pour la méthode pratique que j'ai utilisée au début, cela consiste à remplacer les sommes parfois proches par des montants très différents les uns des autres. On repère alors plus naturellement les problèmes par des incohérences d'ordre de grandeur. En poussant le principe jusqu'au bout, on ne traite même plus de chiffres mais de « quantités ». On a alors les clients qui doivent « une grosse somme », le patron rend une « somme moyenne », que le garçon cherche à conserver en ne rendant qu'un « pouillème ». Ainsi, les clients ont payé légèrement moins que la grosse somme. La note initiale valant ce qu'ils ont payé effectivement plus le pouillème. Dans l'énigme, on cherche à additionner le « légèrement moins gros » avec le « moyen », ce qui donne comme prévu une somme sensiblement plus grosse qui ne correspond à rien.

---

1. ⁽¹⁾ ↑ Dans le second cas, ils ont payés 29,99€ auxquels ont peut ajouter le centime que le garçon leur a consenti.
2. ⁽²⁾ ↑ On remarque que d'un point de vue global, tout s'annule -27 + 2 + 25 = 0. On ne fait aucune création monétaire !
3. ⁽³⁾ ↑ En tout cas certainement pas la signification qu'on cherche à lui donner de « note initiale sans remise »
4. ⁽⁴⁾ ↑ C'est une équation du premier degré : si (a + b = c) alors (a = c – b). Ici a=-30 b=+3 et c=-27