Combien de temps dure un jour, selon vous ?

À priori, vous me répondez vingt-quatre heures. Et vous auriez tort de vous en priver : vous avez en effet raison.
Cet article pourrait s'arrêter là⁽¹⁾, si on ne tenait pas en compte qu'en répondant « vingt-trois heures, cinquante-six minutes et quatre secondes », vous auriez raison aussi…

Comment donc se fait-ce ‽

Eh bien, il faut ici différencier deux « types » de jours : le jour solaire, et le jour stellaire (ou sidéral).

Le jour dont on parle le plus souvent, c'est le jour solaire, vingt-quatre heures, c'est le temps entre deux passages du Soleil au point le plus élevé dans le ciel (passages créés par la rotation de la Terre sur elle-même). C'est sur ce temps qu'est basé notre système de jours, de mois, d'années, etc.
Seulement, la Terre ne fait pas que tourner sur elle-même, elle tourne aussi autour du Soleil. Par conséquent, après un tour sur elle-même, elle n'est plus à la même place. Cela induit que le Soleil n'est plus à la même place dans le ciel :

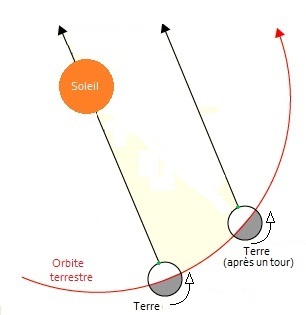
On voit bien ici que, après un tour complet sur elle-même, en partant de midi (par exemple), on arrive le jour suivant un peu avant midi : le laps de temps écoulé est un jour stellaire⁽²⁾.

Pour arriver à midi le jour suivant, il faut encore que la Terre tourne un peu, et que le laps de temps atteigne vingt-quatre heures, soit un jour solaire⁽³⁾.

Pour ceux que seul le phénomène intéresse (et que les calculs embêtent), vous pouvez vous arrêter là. Pour les autres, on va voir comment trouver la durée dudit jour stellaire, par rapport aux vingt-quatre heures du jour solaire⁽⁴⁾.

Bien, pour ceux qui restent (il y en a ?), commençons par fixer la durée d'une année à trois cent soixante-cinq jours et quart (d'où les années bissextiles tous les quatre ans), ce qui correspond à une rotation de la Terre autour du soleil de 360° (un tour complet). On en déduit donc qu'une journée de 24 heures correspond à un angle \(i=\frac{360}{365,25}\approx0,986^\circ\).

Cependant, ce même angle se retrouve aussi entre les droites Terre-Soleil et Terre-étoile fixe :

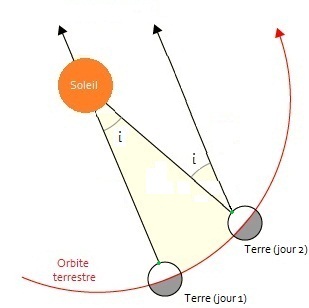
La Terre tourne donc sur elle même d'un angle de \(360 + 0,986 = 360,986°\) pendant un jour solaire (soit vingt-quatre heures, ce qui fait 86 400 secondes), et seulement de 360° pendant un jour stellaire (soit la durée que l'on cherche, nommons-la t, histoire d'être originaux).

Il ne nous reste plus qu'à faire un produit en croix : \(t=\frac{360 \times 86400}{360,986} \approx 86164\) secondes, soit vingt-trois heures, cinquante-six minutes et quatre secondes. On retombe bien sur la valeur que j'ai donné au début, ouf !

---

1. ⁽¹⁾ ↑ Mais vous vous doutez bien qu'on aurait pas fait un article juste pour ça…
2. ⁽²⁾ ↑ On le nomme stellaire – de « étoile » – car pour repérer une direction fixe dans l'espace, on prend comme « point de référence » une étoile lointaine, qui ne bouge apparemment pas.
3. ⁽³⁾ ↑ Puisqu'ici la référence est le Soleil.
4. ⁽⁴⁾ ↑ Et ne vous avisez pas de me dire « on le sait déjà, tu l'as dit au début de l'article ! »…