John Napier⁽¹⁾ était un mathématicien, astronome et physicien écossais.

Célèbre pour avoir inventé les logarithmes⁽²⁾ ainsi que pour l'emploi du point dans les nombres décimaux dans le Royaume-Uni, il possède une unité en génie électrique à son nom⁽³⁾, a également inventé une formule liant les angles d'un triangle sphérique des bâtons⁽⁴⁾, et les bâtons de Napier. Ces bâtons permettent, entre autres, de réaliser facilement des multiplications.

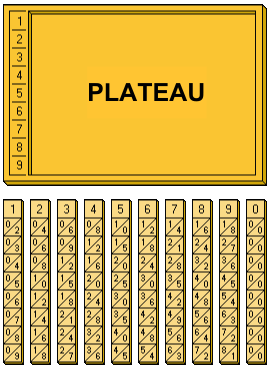
Prenons un exemple de multiplication :

\(2 873 \times 8\)

Pour faire fonctionner les bâtons, nous allons aligner les chiffres (deux, huit, sept et trois) pour former notre nombre. Ensuite, on va lire les résultats affichés pour la huitième ligne, la ligne de la multiplication par huit.

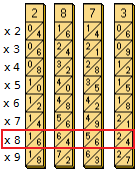
Maintenant, nous allons superposer les résultats selon les contours du motif dessiné par les carrés formés et additionner ce qui se joint :

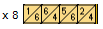
Le \(4\) de droite ne se superpose avec rien. Il tombe donc tout seul. Ensuite, on voit un \(6\) et un \(2\) : ils s'additionnent, soit \(8\). Même chose pour les suivants : \(4 + 5 = 9\), \(6 + 6 = 12\), et enfin, dans le même cas que le \(4\), le \(1\) est tout seul, il le reste. Notre nombre vaut donc : \(4 puis 8 puis 9 puis 12 puis 1\). \(12\) ne peut rester dans cet état, le \(1\) va donc filer en retenue⁽⁵⁾ et le \(1\) qui se trouvait encore seul il n'y a pas dix secondes a désormais un compagnon : ils sont \(2\). Ce qui donne donc : \(4 puis 8 puis 9 puis 2 puis 2.\) Ainsi, on obtient \(22984\).

En vérifiant grâce à la calculatrice, on a bien : \(2873 \times 8 = 22984\)

Eh voilà ! Le mystère des bâtons de Napier est pourtant simple à comprendre. Regardons de plus près ces « chiffres » qui s'ajoutent si mystérieusement, sur l'image précédente. Vous pouvez voir que dans la première colonne de droite, il y a écrit \(2 / 4\). Cela signifie en réalité… \(24\). Cette colonne est celle du \(3\), et vous réalisez donc soudain que : \(8 \times 3 = 24\)
Si Napier a inscrit cette barre qui coupe le nombre en deux, c'est pour permettre justement que le chiffre qui dépasse (en l'occurrence, le \(2\)) puisse s'ajouter au chiffre d'après. Ainsi, vous réalisez une bête addition, mais c'est bien normal : une multiplication est une somme d'additions⁽⁶⁾.

---

1. ⁽¹⁾ ↑ John Neper en français.
2. ⁽²⁾ ↑ Les logarithmes népériens portent son nom.
3. ⁽³⁾ ↑

   Le Néper, Np. Cette unité permet entre autres d'exprimer des voltages et des amplitudes, et il y a une formule permettant de convertir des népers en décibels :

   \(1 Np = \frac{20}{ln(10)} dB \simeq 8,685 dB\)

   \(1 dB = \frac{ln 10}{20} Np \simeq \frac{1}{8,685} \simeq 0,115 Np \)

   D'où :

   \( x Np = \frac{20x}{ln 10} dB \)

   \( x dB = \frac{ln 10 \times x}{20} Np \)

4. ⁽⁴⁾ ↑

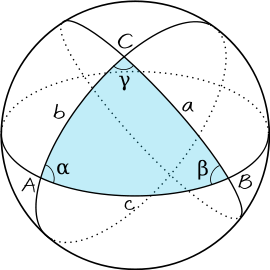   Dans un triangle sphérique \(ABC\), de côtés \(a\), \(b\), \(c\), et d'angles \(\alpha\), \(\beta\), \(\gamma\), la première formule de Napier est une analogie de la formule de la Gauss, et s'écrit sous la forme :

   \(tan \frac{c}{2} cos \frac{\alpha-\beta}{2} = tan\frac{a+b}{2} cos \frac{\alpha + \beta}{2}\)

5. ⁽⁵⁾ ↑ Comprenne qui pourra cet humour scolaire.
6. ⁽⁶⁾ ↑ Les plus avancés diront qu'une puissance est un produit de multiplications : \( x^3 = x \times x \times x \).