Ex nihilo nihil

Des siècles durant, l'Europe refusa le zéro, pourtant si fonctionnel. Les Grecs tout d'abord, du moins les aristotéliciens ; qui prêchaient un monde unique, fini, borné et bourré ; un tas orbitant contre un caillou : la Terre.

L'Église, séduite par les âneries du Grec, s'appropria l'univers unique, compact et borné, puis braya⁽¹⁾ sur ce pré carré. L'Europe devint marque déposée Christus et fonctionna comme nos démocraties : sans crainte du ridicule, par imprécations, par anathèmes.

L'anathème contre le vide freinerait les sciences. Car une valeur nulle était nécessaire au progrès. Sans elle, point de zéro. Et sans zéro, le calcul boitait.

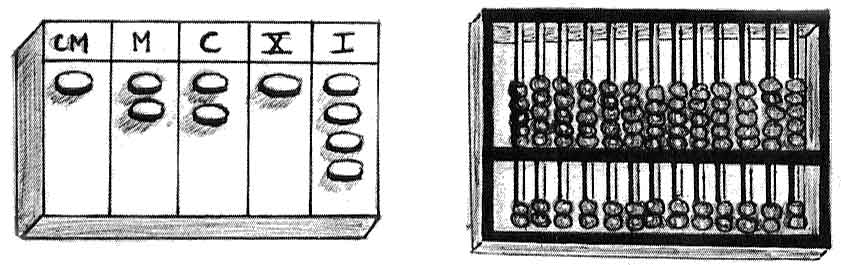
Le zéro connu des Grecs n'était même pas un nombre, mais un marque-place : ce séparateur numérique dont se servaient les Mésopotamiens pour reconnaître leurs nombres. Comme les lignes d'un boulier, sa marque distinguait les quantités exprimées. Elle proportionnait, répartissait, permettait de lire ou écrire sans erreur les nombres ; mais elle n'était qu'une ombre, pas un nombre. L'Orient n'avait pas encore découvert le nombre zéro.

La pensée européenne, obsédée par le Un, excluait tout nombre vide :

L'unité est ce selon quoi chacune des choses existantes est dite une.
Un nombre est un assemblage composé d'unités.

Ainsi, selon ces critères, une valeur nulle était impensable.
Cependant Zéro n'était pas resté parqué entre le Tigre et l'Euphrate. Les Macédoniens, paraît-il, l'emmenèrent rouler sa bosse jusqu'aux Indes, une contrée où les gymnosophistes couchaient sur des planches à clous et où les vaches sacrées larguaient leurs bouses sacrées et leurs dysenteries divines. Les Indiens feraient progresser les mathématiques au cinquième siècle, quand nous vouions encore au seizième des scientifiques au bûcher⁽²⁾.

Si tant est que les méthodes de calcul babyloniennes fussent parvenues en Inde à la suite d'Alexandre, les mathématiciens Indiens y appliquèrent leur génie, donnant au zéro sa valeur de nombre, et fondant le calcul moderne.

Om ! Cela est plénitude ; ceci est plénitude ;
De la plénitude, naît la plénitude.
Quand la plénitude est extraite de la plénitude,
Ce qui reste est encore la plénitude

Comme la Grèce, l'Inde védique est une civilisation du Plein ; mais au contraire des Grecs, elle concevra le Vide et l'intégrera à sa vision. Dans le monde védique tout a sa place, tout est répertorié. Une des six grandes philosophies hindoues, le Sāṃkhya, dénombre vingt-cinq éléments dont est faite la Création ; l'un d'eux, ākāśa (sans limite) désigne l'éther ou espace. L'espace est où il n'y a pas d'air ; il est ce qui est nécessaire à chaque objet de la Manifestation pour trouver sa place. Pour qu'une cerise puisse exister, il lui faut un « espace », éther, adapté exactement à ses proportions, que l'objet soit dense ou subtil ; matériel ou non. Ainsi le terrain indien est propice à la découverte d'un élément nul. Lui a les moyens d'abstraire. La Grèce se focalisait sur la géométrie, le tangible.

En 1881, un inspecteur de police creusant un enclos de pierre dans le village de Bakhshali (Pakistan), exhuma 70 feuillets de bouleau rescapés d'un traité de mathématiques, datant probablement de cette période ; règles d'arithmétique et d'algèbre illustrées d'exemples. L'on y voit la plus ancienne représentation du zéro connue à ce jour :

C'est un point qui représente le zéro : le bindu, création non manifestée mais riche de tous les possibles ; autrement dit, germe de l'Infini.

Au V^e siècle un moine jaïn, Sarvanandî, rédige le Lokavibhâga, traité de Cosmologie. L'ouvrage sera redécouvert sur un manuscrit en date du 25 août 458 (calendrier julien). C'est ici qu'apparaît la position décimale ; zéro n'exprime plus l'absence mais la nullité.

En 498 le mathématicien indien Âryabhata le fait revenir régulièrement de dixième place en dixième place : le système décimal est né. Tel que nous le connaissons.

Avec Brahmagupta (598-668) et son livre, le Brahmasphutasiddhanta (628), les différentes facettes du zéro, chiffre et nombre, sont parfaitement comprises et la construction de notre système décimal parachevée. Les nombres négatifs sont également introduits, ainsi que les racines carrées.

Au IX^e siècle le mathématicien Persan Al-Khwarizmi permet avec son Traité du système de numération des Indiens que les chiffres arabes soient introduits en Occident

Cela se fera au XIII^e siècle par Léonard de Pise qui ramènera son Liber abaci, ses calculs décimaux, de Bougie où il étudiait. Néanmoins son triomphe prendra le temps nécessaire aux esprits pour évoluer, ici quelques siècles, ce qui est plutôt rapide.

---

1. ⁽¹⁾ ↑ Passé simple du verbe braire ! Il vient de naître sur mon clavier et je l'offre humblement à la France et à la Mystique ; puissent-elles avoir autant de simplicité à le recevoir que j'ai de joie à le leur braire.
2. ⁽²⁾ ↑ Témoin Giordano Bruno, qui prétendit infini l'univers et chaque étoile soleil autour duquel des planètes tourneraient.