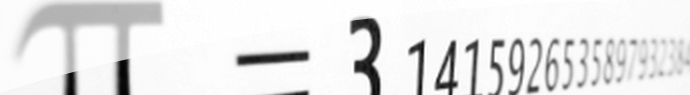
Constantes mathématiques (1) : pi
Informations autour du nombre pi
Voilà le début d'une nouvelle série mathématique, celle des constantes fondamentales mathématiques que l'on rencontre partout !
Nous commençons donc avec \(\pi\). Cette petite merveille, qui vaut environ \(3,14159265\), est connue depuis les Grecs, voire même les Égyptiens.
Cette constante permet de calculer la circonférence d'un cercle de rayon \(R\) (\(2 \pi R\)), l'aire d'un disque de même rayon (\(\pi R^2\)), le volume d'une boule (\(\frac{4}{3}\pi R^3\)).
On définit \(\pi\) comme le double du plus petit nombre positif \(x\) tel que \(cos(x) = 0\).
\(\pi\) est irrationnel (n'est pas le rapport de deux entiers), transcendant (il n'est racine d'aucun polynôme à coefficients rationnels) et on le suppose normal.
Quelques curiosités :
- \(\zeta(2)=\sum_{n=1}^{\infty} \frac{1}{n^2}=\frac{\pi^2}{6}\)
- Cette merveilleuse constante est aussi liée (de façon inversement proportionnelle) à la probabilité qu'une aiguille lancée sur un parquet rencontre deux lattes (expérience dite de l'aiguille de Buffon, du nom de celui qui la réalisa pour la première fois).
Cependant, il reste encore un problème que les mathématiciens n'ont toujours pas résolu au sujet de \(\pi\) : existe-t-il une équation polynomiale à deux variables et à cœfficients entiers dont \(\pi\) et \(e\) soient racines ?