Méthodes de partage… pour ne pas s'arracher les cheveux

Un cheveu
Bon ! n'exagérons rien, on va le couper dans le sens de la longueur…
Trop facile ? pas la peine d'en faire un article. Quoique…

Prenons un bout de ficelle⁽¹⁾, rejoignons les deux extrémités, tirons la boucle, et coupons en tendant : voilà deux belles moitiés.
Et en recommençant, on peut partager en 4 ou 8, 16, 32… \(2^n\) !

Reprenons un autre bout de ficelle⁽²⁾ ! Replions une des extrémités vers le milieu du morceau restant, replions la moitié non recouverte et ajustons : les plis intérieur et extérieur coïncident avec respectivement les brins extérieur et intérieur⁽³⁾.
Vous voilà capable de partager en 3 ou 9, 27, 81… \(3^m\) !
mais aussi en combinant les deux méthodes en 6, 12, 18… en \(2^n \times 3^m\) !

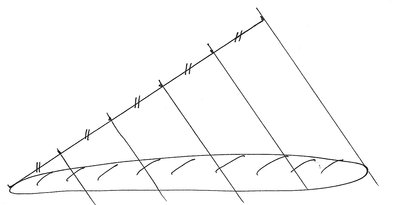
La machine (virtuelle) à trancher les baguettes
Les scrupuleux calculateurs mesurent la longueur totale, puis effectuent la division par le nombre de parts souhaitées… et découpent les parts au millimètre.
Les géomètres imaginatifs visualisent une graduation partant d'une extrémité de la baguette en longueurs identiques et en nombre égal au nombre de parts souhaitées, puis relient virtuellement l'extrémité de la graduation à l'autre extrémité de la baguette, cette direction leur permet de visualiser des parallèles équidistantes qui découpent proprement la baguette comme vous le souhaitiez⁽⁴⁾ !
Un conseil : achetez suffisamment de baguettes et laissez-les à leurs occupations… inadaptées au quotidien.

Une tarte (ou une pizza suivant les goûts)
Non ! on ne va pas massacrer la belle présentation… J'espère qu'avec un couteau, vous allez vous en sortir à vue d'œil⁽⁵⁾.
Vous êtes capable de visualiser le centre ? donc de couper en 2 ? La ligne de coupe est bien droite et passe par le centre ? Bien ! voilà un diamètre… avec le centre, ce sont deux beaux rayons !

Imaginez, accrochez-vous ! imaginez le milieu d'un de ces deux rayons⁽⁶⁾, remontez bien perpendiculairement au diamètre, vous arrivez au bord de la tarte (ou pizza), surtout ne bougez plus !
De ce point, visez le centre et vous obtenez 1/6 de cette tarte (ou pizza). Recommencez et voilà la tarte (ou pizza) partagée en 6…

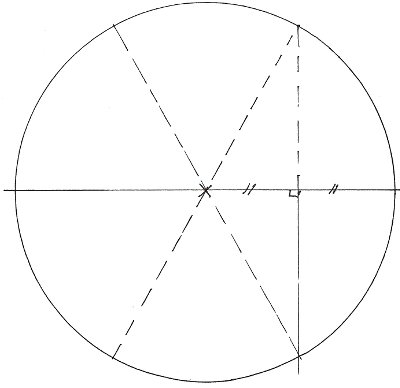
Explication pour matheux pressés : \(\cos(60°) = \frac12\).

Pour les savants cosinus en pantoufles, pliez un triangle équilatéral⁽⁷⁾ en 2, ça peut vous aider à comprendre… Comment pas de triangle équilatéral sous la main ?
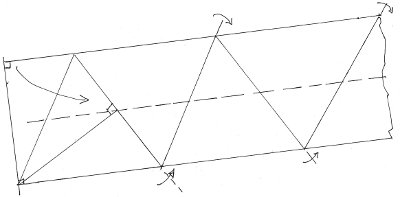
Prenez une bande de papier (deux côtés bien parallèles), vous pouvez préparer la droite médiane en pliant les deux côtés parallèles l'un sur l'autre, dépliez puis coupez une extrémité perpendiculairement (ou repliez un petit bout de bande) pour avoir un bel angle droit, et donc deux, ensuite pliez un de ces angles droits non pas en deux⁽⁸⁾, mais pour que le deuxième angle droit se pose sur la droite médiane. Ainsi vous obtenez un bel angle à 60° que vous repliez sur le côté de la bande une fois d'un côté, une fois de l'autre… comme pour une bande de pâte en fabriquant des samoussas⁽⁹⁾. Et vous voilà avec un beau gabarit de triangle équilatéral !

Zut ! vous la vouliez en 3 ? Ou bien vous visualisez le premier diamètre (en ne coupant qu'un rayon et en prenant le milieu du rayon qui le prolonge… ou bien vous prenez \(\frac26\) chacun⁽¹⁰⁾.
Par contre, maintenant vous coupez comme un chef en 12, 24, 48… en \(2^n \times 3\)⁽¹¹⁾ !

Vous voulez partager en 5 ? Avoir le compas dans l'œil reste la meilleure solution⁽¹²⁾…
Conseil : coupez une part de \(\frac15\), au jugé moins que \(\frac14\) plus que \(\frac16\), et partagez le reste en 4⁽¹³⁾ !

Une tablette de chocolat
Il y a un pré-découpage en général, par exemple 6 barres de 3 « carrés » de chocolat, qui sont pourtant des rectangles non carrés⁽¹⁴⁾ !
Vous voilà avec 18 « carrés » de chocolat que vous pouvez aisément partager en 1 part ou 2, 3, 6, 9 ou 18 parts égales : tous les diviseurs de 18 !

Gâteau de réception
Ce genre de grand pavé rectangulaire se découpe assez bien pourvu que le nombre de parts ait des diviseurs propres⁽¹⁵⁾.
Pour faire 20 parts par exemple, on coupe en 4 sur la largeur et en 5 sur la longueur…
Pour faire 13 parts, on coupe en 13 en longueur (ou en largeur), la forme des parts est moins présentable ! à moins qu'on coupe en 15 parts et les gourmands viendront se resservir…

En deux sans contestation !
Très simple et très efficace ! vous annoncez d'abord la règle du partage : l'un découpe, l'autre choisit sa part… et plus de litiges !

En trois sans garantie…
Une méthode issue d'une théorie mathématique aperçue jadis dans une revue Science et vie : annoncez la règle de partage avant de commencer ; le premier découpe une part, le deuxième partage en deux le gros morceau, le troisième choisit, puis le deuxième et le premier se sert en dernier…

Encore faut-il avoir envie de partager !
Chacun selon ses moyens pour chacun selon ses besoins !

---

1. ⁽¹⁾ ↑ On le voit mieux que le cheveu.
2. ⁽²⁾ ↑ Quand on se cultive, foin des économies de bouts de ficelle…
3. ⁽³⁾ ↑ Certes, ça se fait de façon empirique, mais ça suffit en pratique si la ficelle est fine.
4. ⁽⁴⁾ ↑ Application du fameux théorème de Thalès.
5. ⁽⁵⁾ ↑ Si vous préférez la règle et le compas, aïe ! aïe ! aïe ! je veux bien, mais la présentation va encore souffrir !
6. ⁽⁶⁾ ↑ Donc au quart du diamètre.
7. ⁽⁷⁾ ↑ Celui qui a 3 côtés égaux.
8. ⁽⁸⁾ ↑ Ce serait la bissectrice.
9. ⁽⁹⁾ ↑ Ces petits triangles dégustés avec les nems, les acras et les beignets : dégustez ce petit plat chinois.
10. ⁽¹⁰⁾ ↑ Si vous n'avez pas une ouverture de mâchoire suffisante, autrement dit une grande gueule, vous allez couper votre part pour la déguster de toute façon !
11. ⁽¹¹⁾ ↑ En 9, c'est pas gagné ! parce que même à la règle et au compas la trisection de l'angle, c'est pas de la tarte !… impossible même en français.
12. ⁽¹²⁾ ↑ On peut le faire avec la règle et le compas avec une très bonne visualisation ou un massacre de la présentation.
13. ⁽¹³⁾ ↑ Les parts ne sont pas rigoureusement égales ? Par expérience, il y a toujours un convive rassasié qui en veut une plus petite ou un gourmand qui se réjouit d'une plus grosse…
14. ⁽¹⁴⁾ ↑ Les rectangles carrés, ça existe, un carré est un rectangle… mais oui ! une voiture de course est une voiture.
15. ⁽¹⁵⁾ ↑ Autres que 1 et lui-même, exemple : 4 est un diviseur propre de 12, mais 13 n'a pas de diviseurs propres, ni sales, 13 est un nombre premier.